
【题目】已知函数f(x)=sin(x+ ![]() )+cosx,x∈R,
)+cosx,x∈R,
(1)求函数f(x)的最大值,并写出当f(x)取得最大值时x的取值集合;
(2)若α∈(0, ![]() ),f(α+
),f(α+ ![]() )=
)= ![]() ,求f(2α)的值.
,求f(2α)的值.
【答案】
(1)解:f(x)=sin(x+ ![]() )+cosx=
)+cosx= ![]() sinx+
sinx+ ![]() cosx+cosx=
cosx+cosx= ![]() sinx+
sinx+ ![]() cosx
cosx
= ![]() sin(x+
sin(x+ ![]() ),
),
当x+ ![]() =2kπ+
=2kπ+ ![]() ,
,
即x=2kπ+ ![]() ,k∈Z时,函数f(x)取得最大值
,k∈Z时,函数f(x)取得最大值 ![]() .
.
此时x的取值集合是{x|x=2kπ+ ![]() ,k∈Z}
,k∈Z}
(2)解:由(1)知f(x)= ![]() sin(x+
sin(x+ ![]() ),
),
∵f(α+ ![]() )=
)= ![]() ,
,
∴f(α+ ![]() )=)=
)=)= ![]() sin(
sin( ![]() +α+
+α+ ![]() )=
)= ![]() cosα=
cosα= ![]() ,
,
∴cosα= ![]() ,
,
∵α∈(0, ![]() ),
),
∴sinα= ![]() ,
,
sin2α=2sinαcosα=2× ![]() =
= ![]() ,
,
cos2α=2cos2α﹣1=﹣ ![]() ,
,
∴f(2α)= ![]() =
= ![]() sin2α+
sin2α+ ![]() cos2α=
cos2α= ![]() =
= ![]() .
.
【解析】(1)利用两角和差的正弦公式以及辅助角公式将函数f(x)进行化简,结合三角函数的图象和性质即可求函数f(x)的最大值,并写出当f(x)取得最大值时x的取值集合;(2)根据条件求出sinα和cosα的值,利用二倍角公式进行化简求值.
【考点精析】解答此题的关键在于理解两角和与差的正弦公式的相关知识,掌握两角和与差的正弦公式:![]() .
.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点. 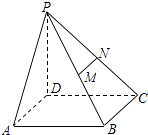
(1)证明:MN∥平面PAD;
(2)若PA与平面ABCD所成的角为45°,求四棱锥P﹣ABCD的体积V.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(sinx,1),
=(sinx,1), ![]() =
= ![]() ,函数f(x)=
,函数f(x)= ![]() 的最大值为6.
的最大值为6.
(1)求A;
(2)将函数f(x)的图象向左平移 ![]() 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的 ![]() 倍,纵坐标不变,得到函数y=g(x)的图象.求g(x)在[0,
倍,纵坐标不变,得到函数y=g(x)的图象.求g(x)在[0, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
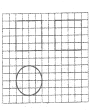
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑,如图,网格纸上正方形小格的边长为![]() ,图中粗线画出的是某几何体毛坯的三视图,第一次切削,将该毛坯得到一个表面积最大的长方体,第二次切削沿长方体的对角面刨开,得到两个三棱柱,第三次切削将两个三棱柱分别沿棱和表面的对角线刨开得到两个鳖臑和两个阳马,则阳马与鳖臑的体积之比为( )
,图中粗线画出的是某几何体毛坯的三视图,第一次切削,将该毛坯得到一个表面积最大的长方体,第二次切削沿长方体的对角面刨开,得到两个三棱柱,第三次切削将两个三棱柱分别沿棱和表面的对角线刨开得到两个鳖臑和两个阳马,则阳马与鳖臑的体积之比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 与圆
与圆![]() :
: ![]() 相切,且与圆
相切,且与圆![]() :
: ![]() 相内切,记圆心
相内切,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .设
.设![]() 为曲线
为曲线![]() 上的一个不在
上的一个不在![]() 轴上的动点,
轴上的动点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 的平行线交曲线
的平行线交曲线![]() 于
于![]() ,
, ![]() 两个不同的点.
两个不同的点.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)试探究![]() 和
和![]() 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
(Ⅲ)记![]() 的面积为
的面积为![]() ,
, ![]() 的面积为
的面积为![]() ,令
,令![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,甲船从A处以每小时30海里的速度沿正北方向航行,乙船在B处沿固定方向匀速航行,B在A北偏西105°方向用与B相距10 ![]() 海里处.当甲船航行20分钟到达C处时,乙船航行到甲船的北偏西120°方向的D处,此时两船相距10海里.
海里处.当甲船航行20分钟到达C处时,乙船航行到甲船的北偏西120°方向的D处,此时两船相距10海里. 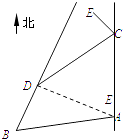
(1)求乙船每小时航行多少海里?
(2)在C的北偏西30°方向且与C相距 ![]() 海里处有一个暗礁E,周围
海里处有一个暗礁E,周围 ![]() 海里范围内为航行危险区域.问:甲、乙两船按原航向和速度航行有无危险?若有危险,则从有危险开始,经过多少小时后能脱离危险?若无危险,请说明理由.
海里范围内为航行危险区域.问:甲、乙两船按原航向和速度航行有无危险?若有危险,则从有危险开始,经过多少小时后能脱离危险?若无危险,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(Ⅰ)当![]() ,求函数
,求函数![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() , 若
, 若![]() 在
在![]() 内恒成立,则称
内恒成立,则称![]() 为函数
为函数![]() 的“类对称点”,当
的“类对称点”,当![]() 时,试问
时,试问![]() 是否存在“类对称点”,若存在,请求出一个“类对称点”的横坐标;若不存在,请说明理由.
是否存在“类对称点”,若存在,请求出一个“类对称点”的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域是
的定义域是![]() ,对于以下四个命题:
,对于以下四个命题:
(1) 若![]() 是奇函数,则
是奇函数,则![]() 也是奇函数;
也是奇函数;
(2) 若![]() 是周期函数,则
是周期函数,则![]() 也是周期函数;
也是周期函数;
(3) 若![]() 是单调递减函数,则
是单调递减函数,则![]() 也是单调递减函数;
也是单调递减函数;
(4) 若函数![]() 存在反函数
存在反函数![]() ,且函数
,且函数![]() 有零点,则函数
有零点,则函数![]() 也有零点.
也有零点.
其中正确的命题共有
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com