过曲线L：y＝x2－1(x＞0)上的点P作L的切线，与坐标轴交于M、N两点，试求P点坐标，使△OMN的面积最小．
直通贵州名校周测月考直通名校系列答案科目：高中数学 来源：高中数学全解题库(国标苏教版·必修4、必修5) 苏教版 题型：044
设P0(x0，y0)为曲线C：y＝x2(x＞0)上的点，过P0作曲线C的切线与x轴交于点Q1，过Ql作平行于y轴的直线与曲线C交于点P1(xl，y1)，然后再过P1作曲线C的切线交x轴于点Q2，过Q2作平行于y轴的直线与曲线C交于点P2(x2，y2)，依此类推，作出以下各点：P0，Q1，P1，Q2，P2，Q3，…，Pn，Qn+l，…．已知x0＝2，设Pn坐标为(xn，yn)(n∈N)．
(1)求出过点P0的切线的方程；
(2)设xn＝f(n)，求f(n)的表达式．
查看答案和解析>>
科目：高中数学 来源：黑龙江省哈师大附中2011－2012学年高二上学期期中考试数学理科试题 题型：044
在圆C：x2＋y2＝4上任取一点P，过P作PD垂直x轴于D，且P与D不重合．
(1)当点P在圆上运动时，线段PD中点M的轨迹E的方程；
(2)直线l：y＝x＋1与(1)中曲线E交于A，B两点，求|AB|的值．
查看答案和解析>>
科目：高中数学 来源：湖南省岳阳市云溪区一中2012届高三第一次模拟考试数学理科试题 题型：044
已知曲线C1：y＝x2－1与x轴相交于A，B两点，与y轴相交于点C，圆C2经过A，B，C三点．
(1)求圆C2的方程；
(2)过点P(0，m)(m＜－1)的直线l与圆C2相切，试探讨直线l与曲线C1的位置关系．
查看答案和解析>>
科目：高中数学 来源：2011年普通高校招生考试湖南卷理数 题型：044
如图，椭圆C1：
＋
＝1(a＞b＞0)的离心率为
，x轴被曲线C2：y＝x2－b截得的线段长等于C1的长半轴长．
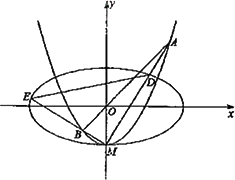
(Ⅰ)求C1，C2的方程；
(Ⅱ)设C2与y轴的焦点为M，过坐标原点O的直线l与C2相交于点A，B，直线MA，MB分别与C1相交与D，E．
(i)证明：MD⊥ME；
(ii)记△MAB，△MDE的面积分别是S1，S2．问：是否存在直线l，使得
＝
？
请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
．
得y2＝
．
，则x1＝
，y2＝－(
)．∴S△OMN＝
·|y2|＝
．把P看成动点，可以把(x0，y0)改写成(x，y)，则S＝
，∴
＝
．令
(负值舍去)．
时，
时，
)．
