
【题目】若关于x的不等式|3x+2|+|3x﹣1|﹣t≥0的解集为R,记实数t的最大值为a.
(1)求a;
(2)若正实数m,n满足4m+5n=a,求 ![]() 的最小值.
的最小值.
【答案】
(1)
解:因为|3x+2|+|3x﹣1|﹣t≥0,所以|3x+2|+|3x﹣1|≥t,
又因为|3x+2|+|3x﹣1|≥|(3x+2)+(1﹣3x)|=3,所以t≤3,
从而实数t的最大值a=3
(2)
解:因为 ![]()
= ![]()
![]() ,
,
所以 ![]() ,从而y≥3,
,从而y≥3,
当且仅当 ![]() ,即
,即 ![]() 时取等号,
时取等号,
所以 ![]() 的最小值为3
的最小值为3
【解析】(1)问题转化为|3x+2|+|3x﹣1|≥t,求出|3x+2|+|3x﹣1|的最小值,从而求出t的范围即可;(2)根据柯西不等式的性质求出函数的最小值即可.
【考点精析】通过灵活运用绝对值不等式的解法,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号即可以解答此题.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)=x|x﹣a|+2x﹣3,其中a∈R
(1)当a=4,2≤x≤5时,求函数f(x)的最大值和最小值,并写出相应的x的值.
(2)若f(x)在R上恒为增函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对100名五年级学生进行了问卷调查,得到如下2×2列联表,平均每天喝500ml以上为常喝,体重超过50kg为肥胖.
不常喝 | 常喝 | 合计 | |
肥胖 | x | y | 50 |
不肥胖 | 40 | 10 | 50 |
合计 | A | B | 100 |
现从这100名儿童中随机抽取1人,抽到不常喝碳酸饮料的学生的概率为 ![]()
(1)求2×2列联表中的数据x,y,A,B的值;
(2)根据列联表中的数据绘制肥胖率的条形统计图,并判断常喝碳酸饮料是否影响肥胖?
(3)是否有99.9%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由. 附:参考公式:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
临界值表:
P(K2≥k) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2011年,国际数学协会正式宣布,将每年的3月14日设为国际数学节,来源是中国古代数学家祖冲之的圆周率.为庆祝该节日,某校举办的数学嘉年华活动中,设计了一个有奖闯关游戏,游戏分为两个环节. 第一环节“解锁”:给定6个密码,只有一个正确,参赛选手从6个密码中任选一个输入,每人最多可输三次,若密码正确,则解锁成功,该选手进入第二个环节,否则直接淘汰.
第二环节“闯关”:参赛选手按第一关、第二关、第三关的顺序依次闯关,若闯关成功,分别获得10个、20个、30个学豆的奖励,游戏还规定,当选手闯过一关后,可以选择带走相应的学豆,结束游戏,也可以选择继续闯下一关,若有任何一关没有闯关成功,则全部学豆归零,游戏结束.设选手甲能闯过第一关、第二关、第三关的概率分别为 ![]() ,选手选择继续闯关的概率均为
,选手选择继续闯关的概率均为 ![]() ,且各关之间闯关成功与否互不影响.
,且各关之间闯关成功与否互不影响.
(1)求某参赛选手能进入第二环节的概率;
(2)设选手甲在第二环节中所得学豆总数为X,求X的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,M,N分别是AB,PC的中点,若ABCD是平行四边形.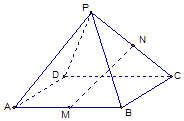
(1)求证:MN∥平面PAD.
(2)若PA=AD=2a,MN与PA所成的角为30°.求MN的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数F(x)=xf(x),f(x)满足f(x)=f(﹣x),且当x∈(﹣∞,0]时,F'(x)<0成立,若 ![]() ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )
A.a>b>c
B.c>a>b
C.c>b>a
D.a>c>b
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,且∠ABC=120°.点E是棱PC的中点,平面ABE与棱PD交于点F. (Ⅰ)求证:AB∥EF;
(Ⅱ)若PA=PD=AD=2,且平面PAD⊥平面ABCD,求平面PAF与平面AEF所成的二面角的正弦值.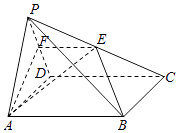
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an+1=1﹣ ![]() ,其中n∈N* .
,其中n∈N* .
(Ⅰ)设bn= ![]() ,求证:数列{bn}是等差数列,并求出{an}的通项公式an;
,求证:数列{bn}是等差数列,并求出{an}的通项公式an;
(Ⅱ)设Cn= ![]() ,数列{CnCn+2}的前n项和为Tn , 是否存在正整数m,使得Tn<
,数列{CnCn+2}的前n项和为Tn , 是否存在正整数m,使得Tn< ![]() 对于n∈N*恒成立,若存在,求出m的最小值,若不存在,请说明理由.
对于n∈N*恒成立,若存在,求出m的最小值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com