
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,且
,且![]() 平面
平面![]() ,
,![]() ,M,N分别为
,M,N分别为![]() ,
,![]() 的中点.
的中点.

(1)记平面![]() 与底面
与底面![]() 的交线为l,试判断直线l与平面
的交线为l,试判断直线l与平面![]() 的位置关系,并证明.
的位置关系,并证明.
(2)点Q在棱![]() 上,若Q到平面
上,若Q到平面![]() 的距离为
的距离为![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)直线![]() 平面
平面![]() ,证明见解析.(2)
,证明见解析.(2)![]() .
.
【解析】
(1)连接![]() ,可由线面平行判定定理证明
,可由线面平行判定定理证明![]() 平面
平面![]() ,再由线面平行性质及平行线的传递性证明直线
,再由线面平行性质及平行线的传递性证明直线![]() 与平面
与平面![]() 平行即可.
平行即可.
(2)以A为原点建立空间直角坐标系,写出各个点的坐标,并设![]() ,
,![]() ,结合坐标运算可用
,结合坐标运算可用![]() 表示
表示![]() 的坐标,并求得平面
的坐标,并求得平面![]() 的法向量.根据条件及点到平面距离的向量求法,即可确定
的法向量.根据条件及点到平面距离的向量求法,即可确定![]() 的值,进而求得线段
的值,进而求得线段![]() 的长.
的长.
(1)直线![]() 与平面
与平面![]() 平行,证明如下:
平行,证明如下:
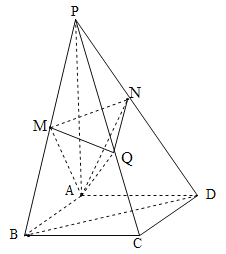
连接![]() ,如下图所示:
,如下图所示:
M,N分别为![]() ,
,![]() 的中点,
的中点,
则由中位线定理可得![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
平面![]() 与底面
与底面![]() 的交线为
的交线为![]() ,
,
由线面平行的性质可得![]() ,
,
又因为![]() ,
,
则由平行线传递性可得![]()
因为![]() ,且
,且![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以直线![]() 平面
平面![]() .
.
(2)根据题意,以A为原点,建立如下图所示的空间直角坐标系:
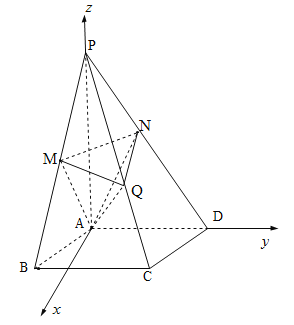
则![]()
![]() 设
设![]() ,
,![]() ,(
,(![]() ),
),
所以![]()
解得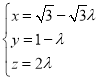 ,所以
,所以![]()
则由中点坐标公式可得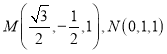 ,
,
则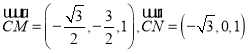
设平面![]() 的法向量为
的法向量为![]() ,
,
则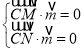 ,即
,即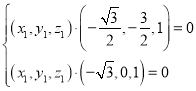
所以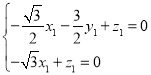 ,令
,令![]() ,代入解得
,代入解得![]() .
.
即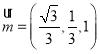
而![]() ,
,
所以Q到平面![]() 的距离
的距离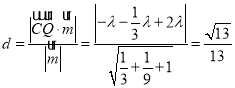 ,
,
解得![]() ,因为
,因为![]() ,
,
所以![]() .
.
所以![]()


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,离心率为
,离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 上的一个动点,且
上的一个动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 斜率为
斜率为![]() ,且
,且![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 若存在,求
若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过抛物线![]() 上的一点
上的一点![]() 作抛物线的切线,分别交x轴于点D交y轴于点B,点Q在抛物线上,点E,F分别在线段AQ,BQ上,且满足
作抛物线的切线,分别交x轴于点D交y轴于点B,点Q在抛物线上,点E,F分别在线段AQ,BQ上,且满足![]() ,
,![]() ,线段QD与
,线段QD与![]() 交于点P.
交于点P.

(1)当点P在抛物线C上,且![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() 是线段
是线段![]() 上的动点,则下列说法错误的是( )
上的动点,则下列说法错误的是( )

A. 当点![]() 移动至
移动至![]() 中点时,直线
中点时,直线![]() 与平面
与平面![]() 所成角最大且为
所成角最大且为![]()
B. 无论点![]() 在
在![]() 上怎么移动,都有
上怎么移动,都有![]()
C. 当点![]() 移动至
移动至![]() 中点时,才有
中点时,才有![]() 与
与![]() 相交于一点,记为点
相交于一点,记为点![]() ,且
,且![]()
D. 无论点![]() 在
在![]() 上怎么移动,异面直线
上怎么移动,异面直线![]() 与
与![]() 所成角都不可能是
所成角都不可能是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】时值金秋十月,正是秋高气爽,阳光明媚的美好时刻。复兴中学一年一度的校运会正在密锣紧鼓地筹备中,同学们也在热切地期盼着,都想为校运会出一份力。小智同学则通过对学校有关部门的走访,随机地统计了过去许多年中的五个年份的校运会“参与”人数及相关数据,并进行分析,希望能为运动会组织者科学地安排提供参考。
附:①过去许多年来学校的学生数基本上稳定在3500人左右;②“参与”人数是指运动员和志愿者,其余同学均为“啦啦队员”,不计入其中;③用数字1、2、3、4、5表示小智同学统计的五个年份的年份数,今年的年份数是6;
统计表(一)
年份数x | 1 | 2 | 3 | 4 | 5 |
“参与”人数(y千人) | 1.9 | 2.3 | 2.0 | 2.5 | 2.8 |
统计表(二)
高一(3)(4)班参加羽毛球比赛的情况:
男生 | 女生 | 小计 | |
参加(人数) | 26 | b | 50 |
不参加(人数) | c | 20 | |
小计 | 44 | 100 |
(1)请你与小智同学一起根据统计表(一)所给的数据,求出“参与”人数y关于年份数x的线性回归方程![]() ,并预估今年的校运会的“参与”人数;
,并预估今年的校运会的“参与”人数;
(2)学校命名“参与”人数占总人数的百分之八十及以上的年份为“体育活跃年”.如果该校每届校运会的“参与”人数是互不影响的,且假定小智同学对今年校运会的“参与”人数的预估是正确的,并以这6个年份中的“体育活跃年”所占的比例作为任意一年是“体育活跃年”的概率。现从过去许多年中随机抽取9年来研究,记这9年中“体活跃年”的个数为随机变量![]() ,试求随机变量
,试求随机变量的分布列、期望
![]() 和方差
和方差![]() ;
;
(3)根据统计表(二),请问:你能否有超过60%的把握认为“羽毛球运动”与“性别”有关?
参考公式和数据一: ,
,![]() ,
,![]() ,
,![]()
参考公式二: ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com