练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图2-22,已知两圆相交于C、D,AB为公切线,CD的延长线交AB于M,若AB=12,CD=9,则MD=________________.

    图2-22

    解析:由切割线定理,MA2=MD·MC,MB2=MD·MC,

    ∴MA2=MB2.

    ∴MA=MB=AB=6.

    ∵MA2=MD·MC,

    ∴62=MD(MD+9).解得MD=3.

    答案:3

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网如图，已知椭圆
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    的离心率为
    		2
    2
    ，其右焦点F是圆（x-1）2+y2=1的圆心．
    （1）求椭圆方程；
    （2）过所求椭圆上的动点P作圆的两条切线分别交y轴于M（0，m），N（0，n）两点，当|m-n|=2
    		2
    -1
    时，求此时点P的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，某城市设立以城中心O为圆心、r公里为半径的圆形保护区，从保护区边缘起，在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC，现要在保护区边缘PQ弧上选择一点A作为出口，建一条连接两条公路且与圆O相切的直道BC．已知通往一级公路的道路AC每公里造价为a万元，通往高速公路的道路AB每公里造价是m2a万元，其中a，r，m为常数，设∠POA=θ，总造价为y万元．
    （1）把y表示成θ的函数y=f（θ），并求出定义域；
    （2）当m=
    		6
    +
    		2
    2
    时，如何确定A点的位置才能使得总造价最低？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

     选做题（在A、B、C、D四小题中只能选做两题，并将选作标记用2B铅笔涂黑，每小题10分，共20分，请在答题指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）．
    A、（选修4-1：几何证明选讲）
    如图，BD为⊙O的直径，AB=AC，AD交BC于E，求证：AB2=AE•AD
    B、（选修4-2：矩形与变换）
    已知a，b实数，如果矩阵M=
    1a
    b2
    所对应的变换将直线3x-y=1变换成x+2y=1，求a，b的值．
    C、（选修4-4，：坐标系与参数方程）
    设M、N分别是曲线ρ+2sinθ=0和ρsin（θ+
    π
    4
    ）=
    		2
    2
    上的动点，判断两曲线的位置关系并求M、N间的最小距离．
    D、（选修4-5：不等式选讲）
    设a，b，c是不完全相等的正数，求证：a+b+c＞
    		ab
    +
    		bc
    +
    		ca
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    己知在锐角ΔABC中，角所对的边分别为，且

    (I )求角大小；

    (II)当时，求的取值范围.

    20．如图1，在平面内，是的矩形，是正三角形，将沿折起，使如图2，为的中点，设直线过点且垂直于矩形所在平面，点是直线上的一个动点，且与点位于平面的同侧。

    （1）求证：平面；

    （2）设二面角的平面角为，若，求线段长的取值范围。

     


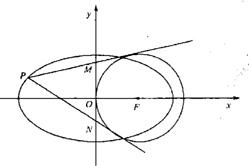
    21.已知A，B是椭圆的左，右顶点，，过椭圆C的右焦点F的直线交椭圆于点M，N，交直线于点P，且直线PA，PF，PB的斜率成等差数列,R和Q是椭圆上的两动点，R和Q的横坐标之和为2，RQ的中垂线交X轴于T点

    (1)求椭圆C的方程；

    （2）求三角形MNT的面积的最大值

    22. 已知函数 ，

    （Ⅰ）若在上存在最大值与最小值，且其最大值与最小值的和为，试求和的值。

    （Ⅱ）若为奇函数：

    （1）是否存在实数，使得在为增函数，为减函数，若存在，求出的值，若不存在，请说明理由；

    （2）如果当时，都有恒成立，试求的取值范围.

    查看答案和解析>>

    同步练习册答案