练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在△ABC中，已知角A、B、C所对的边分别是a、b、c，边c=，且tanA+tanB=tanA·tanB－，又△ABC的面积为S△ABC=，求a+b的值。（本题满分12分）

     

    【答案】

    解：由tanA+tanB=tanA·tanB－可得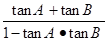＝－，………（3分）新 课 标 第一网

    即tan(A+B)=－                                    …………………….（4分）

    ∴tan(π－C)= －, ∴－tanC=－, ∴tanC=

    ∵C∈(0, π), ∴C=……………………………………………………….（6分）

    又△ABC的面积为S△ABC=，∴absinC=即ab×=, ∴ab=6…….（8分）

    又由余弦定理可得c2=a2+b2－2abcosC

    ∴()2= a2+b2－2abcos∴()2= a2+b2－ab=(a+b)2－3ab∴(a+b)2=,   …….（11分）

     ∵a+b>0,   ∴a+b=     ……………………………………………………. (12分)

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在△ABC中，已知角A，B，C的对边分别为a，b，c，若A，B，C成等差数列，且b=
    		3
    ，c=
    		2
    ，则B=
     
    ，A=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，已知角A为锐角，角A、B、C的对边分别为a、b、c，sinA=
    2
    		2
    3
    ．
    （1）求tan2
    B+C
    2
    +sin2
    A
    2
    的值；
    （2）若a=2
    		2
    ，S△ABC=
    		2
    ，求b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，已知角A、B、C对应的三边分别为a，b，c，满足（a+b+c）（a+b-c）=3ab，则角C的大小等于
    π
    3
    π
    3
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，已知角A，B，C满足2B=A+C，且tanA和tanB是方程x2-λx+λ+1=0的两根，若△ABC的面积为3+
    		3
    ，试求△ABC的三边的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，已知角A，B，C的对边分别是a，b，c，且a2+b2-c2=
    		3
    ab    ．
    （1）求角C的大小；
    （2）如果0＜A≤
    2π
    3
    ，m=2cos2
    A
    2
    -sinB-1    ，求实数m的取值范围．

    查看答案和解析>>

    同步练习册答案