
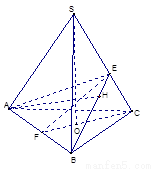
已知三棱锥S—ABC的底面是正三角形,A点在侧面SBC上的射影H是△SBC的垂心.
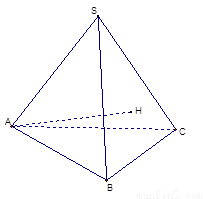
(1)求证:BC⊥SA
(2)若S在底面ABC内的射影为O,证明:O为底面△ABC的中心;
(3)若二面角H—AB—C的平面角等于30°,SA=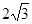 ,求三棱锥S—ABC的体积.
,求三棱锥S—ABC的体积.
(1)先证明 (2)
先证O为底面△ABC的垂心 (3)
(2)
先证O为底面△ABC的垂心 (3)
【解析】
试题分析:证明:(1)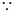 AH⊥面SBC,BC在面SBC内 ∴AH⊥BC
AH⊥面SBC,BC在面SBC内 ∴AH⊥BC
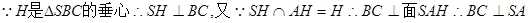
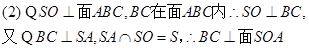
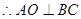 ,同理
,同理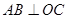 ,因此
,因此
|
O为底面△ABC的垂心,而三棱锥S—ABC的底面是正三角形,故O为底面△ABC的中心
(3)由(1)有SA=SB=SC=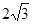 ,设CO交AB于F,则CF⊥AB, CF是EF在面ABC内的射影,
,设CO交AB于F,则CF⊥AB, CF是EF在面ABC内的射影,
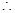 EF⊥AB,
EF⊥AB,
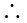 ∠EFC为二面角H—AB—C的平面角,∠EFC=30°,∠ECF=60°,
∠EFC为二面角H—AB—C的平面角,∠EFC=30°,∠ECF=60°,
OC=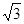 ,SO=3,AB=3,
,SO=3,AB=3,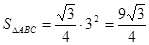

考点:直线与平面垂直的性质;棱柱、棱锥、棱台的体积.
点评:本题考查异面直线垂直的证明,考查三角形中心的证明,考查三棱锥体积的求法,解题时要认真审题,仔细解答,合理地化空间问题为平面问题.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
| 2 |
| A、π | B、2π | C、3π | D、4π |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com