
分析 (1)求出${f^'}(x)=\frac{{(1-2x){e^{2x}}}}{{{{({e^{2x}})}^2}}}=(1-2x){e^{-2x}}$,利用导数性质能求出f(x)的单调区间、最大值.
(2)设$g(x)=\frac{x}{{{e^{2x}}}}+c$,h(x)=|lnx|,由${g}^{'}(x)=\frac{1-2x}{{e}^{2x}}$,由此根据c>0,c=0,c<0三种情况进行分类讨论,能求出关于x的方程|lnx|=f(x)+c根的个数.
解答 解:(1)∵函数$f(x)=\frac{x}{{{e^{2x}}}}$,
∴${f^'}(x)=\frac{{(1-2x){e^{2x}}}}{{{{({e^{2x}})}^2}}}=(1-2x){e^{-2x}}$,
∴$x∈(-∞,\frac{1}{2})$时,函数f(x)单调递增,$x∈(\frac{1}{2},+∞)$时,函数f(x)单调递减,
∴$f{(x)_{max}}=f(\frac{1}{2})=\frac{1}{2e}$.
(2)设$g(x)=\frac{x}{{{e^{2x}}}}+c$,
①当c>0时,令${g^'}(x)=\frac{1-2x}{{{e^{2x}}}}=0⇒x=\frac{1}{2}$,
当$x∈(0,\frac{1}{2})$时,g′(x)>0;当$x∈(\frac{1}{2},+∞)$时,g′(x)<0;
∴g(x)在$x=\frac{1}{2}$处取极大值$g(\frac{1}{2})=\frac{1}{2e}+c$,
设h(x)=|lnx|
∵自然对数lnx在x>0上单调增,0<x<1时,lnx<0,x≥1时,lnx≥0,
∴0<x<1时,h(x)>0,单调减,x≥1时,h(x)≥0,单调增,
∴h(x)图象与g(x)图象必存在二个交点,即方程|lnx|=g(x)必有二个根;
②当c=0时,
∵方程|lnx|=g(x),
设H(x)=|lnx|-g(x),
写成分段函数:$H(x)=-lnx-\frac{x}{{{e^{2x}}}}-c$,(0<x<1)$H(x)=lnx-\frac{x}{{{e^{2x}}}}-c$,(x≥1)
当0<x<1时,${H^'}(x)=-\frac{1}{x}-\frac{1-2x}{{{e^{2x}}}}<0$,∴h(x)单调减;$H(\frac{1}{2})=ln2-\frac{1}{2e}>0$,$h(1)=-\frac{1}{e^2}<0$,
∴在区间$[\frac{1}{2},1]$一必有一个实根;
当x≥1时,${H^'}(x)=\frac{1}{x}-\frac{1-2x}{{{e^{2x}}}}>0$,∴h(x)单调增;$H(2)=ln2-\frac{2}{e^4}>0$,
∴在区间[1,2]一必有一个实根,
∴当c=0时,h(x)必有二个实根,即方程|lnx|=g(x)必有二个根,③
③当c<0时,
令$g(1)=\frac{1}{e^2}+c=0⇒c=-\frac{1}{e^2}$,
∴$c=-\frac{1}{e^2}$时,h(x)图象与g(x)图象必存在在一个交点,即方程|lnx|=g(x)必有一个根,
综上:当$c>-\frac{1}{e^2}$时,方程|lnx|=g(x)必有二个根;
当$c=-\frac{1}{e^2}$时,方程|lnx|=g(x)必有一个根;
当$c<-\frac{1}{e^2}$时,方程|lnx|=g(x)无实根.
点评 本题考查函数的单调区间、最大值的求法,考查方程的根的个数的求不地,是中档题,解题时要认真审题,注意导数性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $2\sqrt{34}$ | B. | 10 | C. | $8\sqrt{2}$ | D. | $6\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
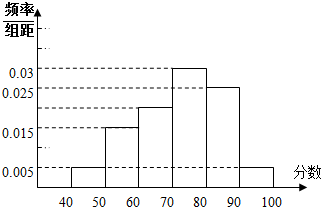 某校从参加高二学业水平考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),[70,80)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高二学业水平考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),[70,80)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | $\frac{{\sqrt{3}}}{3}$ | D. | -$\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{4a},0)$ | B. | $(0,\frac{1}{16a})$ | C. | $(0,-\frac{1}{16a})$ | D. | $(\frac{1}{16a},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com