
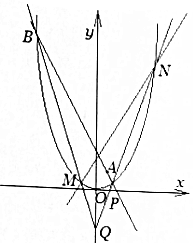
 已知过点P($\frac{1}{2}$,0)的直线l与抛物线x2=y交于不同的两点A,B,点Q(0,-1),连接AQ、BQ的直线与抛物线的另一交点分别为N,M,如图所示.
已知过点P($\frac{1}{2}$,0)的直线l与抛物线x2=y交于不同的两点A,B,点Q(0,-1),连接AQ、BQ的直线与抛物线的另一交点分别为N,M,如图所示.分析 (1)设直线l的方程为:x=my+$\frac{1}{2}$,A(x1,y1),B(x2,y2),联立$\left\{\begin{array}{l}{x=my+\frac{1}{2}}\\{{x}^{2}=y}\end{array}\right.$,得${m}^{2}{y}^{2}+(m-1)y+\frac{1}{4}=0$,
$\left\{\begin{array}{l}{{y}_{1}+{y}_{2}=\frac{1-m}{{m}^{2}}}\\{{y}_{1}{y}_{2}=\frac{\frac{1}{4}}{{m}^{2}}}\\{△=1-2m>0}\end{array}\right.$,…①,由$\overrightarrow{PB}$=2$\overrightarrow{PA}$,得y2=2y1…②
由①②得m即可.
(2)设PQ:y+1=$\frac{{y}_{1}+1}{{x}_{1}}x$
由$\left\{\begin{array}{l}{y+1=\frac{{y}_{1}+1}{{x}_{1}}x}\\{{x}^{2}=y}\end{array}\right.$得${x}_{1}{x}^{2}-({y}_{1}+1)x+{x}_{1}=0$,⇒${x}_{N=\frac{1}{{x}_{1}}},{y}_{N}={{x}_{N}}^{2}$
同理x${x}_{M}=\frac{1}{{x}_{2}},{y}_{M}={{x}_{M}}^{2}$;
直线MN的斜率kMN=$\frac{m({y}_{1}+{y}_{2})+1}{{m}^{2}{y}_{1}{y}_{2}+\frac{m}{2}({y}_{1}+{y}_{2})+\frac{1}{4}}$…③
把①代入③得kMN
解答 解:(1)设直线l的方程为:x=my+$\frac{1}{2}$,A(x1,y1),B(x2,y2)
联立$\left\{\begin{array}{l}{x=my+\frac{1}{2}}\\{{x}^{2}=y}\end{array}\right.$,得${m}^{2}{y}^{2}+(m-1)y+\frac{1}{4}=0$,
$\left\{\begin{array}{l}{{y}_{1}+{y}_{2}=\frac{1-m}{{m}^{2}}}\\{{y}_{1}{y}_{2}=\frac{\frac{1}{4}}{{m}^{2}}}\\{△=1-2m>0}\end{array}\right.$,…①
∵$\overrightarrow{PB}$=2$\overrightarrow{PA}$,∴y2=2y1…②
由①②得${y}_{1}=\frac{1-m}{3{m}^{2}},{{y}_{1}}^{2}=\frac{1}{8{m}^{2}}$,
解得m=-8+6$\sqrt{2}$<$\frac{1}{2}$,m=-8-6$\sqrt{2}$<$\frac{1}{2}$,
∴直线l的斜率的斜率为:1$±\frac{3\sqrt{2}}{4}$.
(2)设PQ:y+1=$\frac{{y}_{1}+1}{{x}_{1}}x$
由$\left\{\begin{array}{l}{y+1=\frac{{y}_{1}+1}{{x}_{1}}x}\\{{x}^{2}=y}\end{array}\right.$得${x}_{1}{x}^{2}-({y}_{1}+1)x+{x}_{1}=0$,⇒${x}_{N}=\frac{1}{{x}_{1}},{y}_{N}={{x}_{N}}^{2}$
同理x${x}_{M}=\frac{1}{{x}_{2}},{y}_{M}={{x}_{M}}^{2}$;
直线MN的斜率kMN=$\frac{{y}_{M}-{y}_{N}}{{x}_{M}-{x}_{N}}=\frac{{{x}_{M}}^{2}-{{x}_{N}}^{2}}{{x}_{M}-{x}_{N}}={x}_{M}+{x}_{N}$
=$\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}}=\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{m({y}_{1}+{y}_{2})+1}{{m}^{2}{y}_{1}{y}_{2}+\frac{m}{2}({y}_{1}+{y}_{2})+\frac{1}{4}}$…③
把①代入③得kMN=2(定值)
∴直线MN的斜率是为定值2.
点评 本题考查了直线与抛物线的位置关系,解题关键合理运用韦达定理,及方程思想,属于压轴题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|x<0} | B. | {x|x>1} | C. | {x|0<x<1} | D. | {x|0<x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
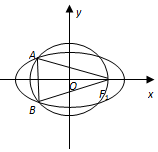 如图,F1是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点,A和B是以O为圆心,以|OF1|为半径的圆与该左半椭圆的两个交点,且△F1AB是等边三角形,求椭圆的离心率.
如图,F1是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点,A和B是以O为圆心,以|OF1|为半径的圆与该左半椭圆的两个交点,且△F1AB是等边三角形,求椭圆的离心率.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b,则ac2>bc2 | B. | 若a>b>0,c>d>0,则$\frac{a}{d}>\frac{b}{c}$ | ||
| C. | 若a<b<0,则ab<b2 | D. | 若$\frac{a}{b}>1$,则a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{1}{2}$ | C. | 1 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com