
设椭圆 =1(a>b>0)的左焦点为F,离心率为
=1(a>b>0)的左焦点为F,离心率为 ,过点F且与x轴垂直的直线被椭圆截得的线段长为
,过点F且与x轴垂直的直线被椭圆截得的线段长为 .
.
(1)求椭圆的方程;
(2)设A,B分别为椭圆的左、右顶点,过点F且斜率为k的直线与椭圆交于C,D两点.若 +
+ =8,求k的值.
=8,求k的值.
(1) =1.(2)k=±
=1.(2)k=± .
.
【解析】(1)设F(-c,0),由 =
= ,知a=
,知a= c.过点F且与x轴垂直的直线为x=-c,代入椭圆方程有
c.过点F且与x轴垂直的直线为x=-c,代入椭圆方程有 =1,解得y=±
=1,解得y=±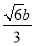 ,于是
,于是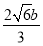 =
=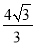 ,解得b=
,解得b= ,又a2-c2=b2,从而a=
,又a2-c2=b2,从而a= ,c=1,
,c=1,
所以椭圆的方程为 =1.
=1.
(2)设点C(x1,y1),D(x2,y2),由F(-1,0)得直线CD的方程为y=k(x+1),由方程组 消去y,整理得(2+3k2)x2+6k2x+3k2-6=0.由根与系数的关系可得x1+x2=-
消去y,整理得(2+3k2)x2+6k2x+3k2-6=0.由根与系数的关系可得x1+x2=-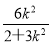 ,x1x2=
,x1x2= ,因为A(-
,因为A(- ,0),B(
,0),B( ,0),所以
,0),所以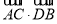 +
+ =(x1+
=(x1+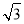 ,y1)·(
,y1)·(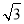 -x2,-y2)+(x2+
-x2,-y2)+(x2+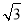 ,y2)·(
,y2)·( -x1,-y1)=6-2x1x2-2y1y2=6-2x1x2-2k2(x1+1)(x2+1)=6-(2+2k2)x1x2-2k2(x1+x2)-2k2=6+
-x1,-y1)=6-2x1x2-2y1y2=6-2x1x2-2k2(x1+1)(x2+1)=6-(2+2k2)x1x2-2k2(x1+x2)-2k2=6+ .由已知得6+
.由已知得6+ =8,解得k=±
=8,解得k=± .
.


科目:高中数学 来源:2014年高考数学(理)二轮复习专题能力测评1练习卷(解析版) 题型:选择题
已知函数f(x)= 则满足f(x)≤2的x的取值范围是( ).
则满足f(x)≤2的x的取值范围是( ).
A.[-1,2] B.[0,2] C.[1,+∞) D.[-1,+∞)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练18练习卷(解析版) 题型:填空题
一出租车司机从饭店到火车站的途中经过六个交通岗,假设他在各交通岗遇到红灯这一事件是相互独立的,并且概率都是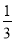 .那么这位司机遇到红灯前,已经通过了两个交通岗的概率是________.
.那么这位司机遇到红灯前,已经通过了两个交通岗的概率是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练17练习卷(解析版) 题型:选择题
某学校有男、女学生各500名,为了解男、女学生在学习兴趣与业余爱好方面是否存在显著差异,拟从全体学生中抽取100名学生进行调查,则宜采用的抽样方法是( ).
A.抽签法 B.随机数法 C.系统抽样法 D.分层抽样法
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(解析版) 题型:选择题
过抛物线y2=2px(p>0)的焦点F且倾斜角为60°的直线l与抛物线分别交于A,B两点,则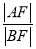 的值等于( ).
的值等于( ).
A.5 B.4 C.3 D.2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:解答题
在平面直角坐标系xOy中,曲线y=x2-6x+1与坐标轴的交点都在圆C上.
(1)求圆C的方程;
(2)若圆C与直线x-y+a=0交于A,B两点,且OA⊥OB,求a的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练13练习卷(解析版) 题型:选择题
已知正三棱柱ABC-A1B1C1的侧棱长与底面边长相等,则AB1与侧面ACC1A1所成角的正弦等于( ).

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷5练习卷(解析版) 题型:解答题
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点.
(1)求椭圆C的方程;
(2)是否存在平行于OA的直线l,使得直线l与椭圆C有公共点,且直线OA与l的距离等于4?若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com