
在平面直角坐标系xOy中,曲线y=x2-6x+1与坐标轴的交点都在圆C上.
(1)求圆C的方程;
(2)若圆C与直线x-y+a=0交于A,B两点,且OA⊥OB,求a的值.
(1)(x-3)2+(y-1)2=9.(2)a=-1.
【解析】(1)曲线y=x2-6x+1与坐标轴的交点为(0,1),(3±2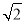 ,0).故可设圆心坐标为(3,t),
,0).故可设圆心坐标为(3,t),
则有32+(t-1)2=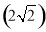 2+t2.
2+t2.
解得t=1,则圆的半径为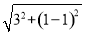 =3.
=3.
所以圆的方程为(x-3)2+(y-1)2=9.
(2)设A(x1,y1),B(x2,y2),其坐标满足方程组 ,
,
消去y得到方程2x2+(2a-8)x+a2-2a+1=0,
由已知可得判别式Δ=56-16a-4a2>0,
由根与系数的关系可得x1+x2=4-a,x1x2=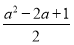 ,①
,①
由OA⊥OB可得x1x2+y1y2=0.又y1=x1+a,y2=x2+a.所以2x1x2+a(x1+x2)+a2=0.
由①②可得a=-1,满足Δ>0,故a=-1.


 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练9练习卷(解析版) 题型:选择题
在等差数列{an}中,a1=-2 014,其前n项和为Sn,若 =2,则S2 014的值等于( ).
=2,则S2 014的值等于( ).
A.-2 011 B.-2 012 C.-2 014 D.-2 013
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练17练习卷(解析版) 题型:填空题
某校开展“爱我海西、爱我家乡”摄影比赛,9位评委为参赛作品A给出的分数如茎叶图所示.记分员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是________.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练15练习卷(解析版) 题型:解答题
设椭圆 =1(a>b>0)的左焦点为F,离心率为
=1(a>b>0)的左焦点为F,离心率为 ,过点F且与x轴垂直的直线被椭圆截得的线段长为
,过点F且与x轴垂直的直线被椭圆截得的线段长为 .
.
(1)求椭圆的方程;
(2)设A,B分别为椭圆的左、右顶点,过点F且斜率为k的直线与椭圆交于C,D两点.若 +
+ =8,求k的值.
=8,求k的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练15练习卷(解析版) 题型:选择题
已知双曲线C与椭圆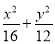 =1有共同的焦点F1,F2,且离心率互为倒数.若双曲线右支上一点P到右焦点F2的距离为4,则PF2的中点M到坐标原点O的距离等于( ).
=1有共同的焦点F1,F2,且离心率互为倒数.若双曲线右支上一点P到右焦点F2的距离为4,则PF2的中点M到坐标原点O的距离等于( ).
A.3 B.4 C.2 D.1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:选择题
直线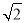 ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).
ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).
A.0 B. C.
C. -1 D.
-1 D. +1
+1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练13练习卷(解析版) 题型:解答题
如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.
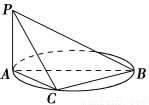
(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求二面角C?PB?A的余弦值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练12练习卷(解析版) 题型:选择题
已知m和n是两条不同的直线,α和β是两个不重合的平面,那么下面给出的条件中一定能推出m⊥β的是( ).
A.α⊥β,且m?α B.m∥n,且n⊥β
C.α⊥β,且m∥α D.m⊥n,且n∥β
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷5练习卷(解析版) 题型:选择题
已知过A(-1,a),B(a,8)两点的直线与直线2x-y+1=0平行,则a的值为( ).
A.-10 B.17 C.5 D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com