
已知双曲线C与椭圆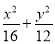 =1有共同的焦点F1,F2,且离心率互为倒数.若双曲线右支上一点P到右焦点F2的距离为4,则PF2的中点M到坐标原点O的距离等于( ).
=1有共同的焦点F1,F2,且离心率互为倒数.若双曲线右支上一点P到右焦点F2的距离为4,则PF2的中点M到坐标原点O的距离等于( ).
A.3 B.4 C.2 D.1
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练9练习卷(解析版) 题型:解答题
已知公差不为零的等差数列{an}的前4项和为10,且a2,a3,a7成等比数列.
(1)求通项公式an;
(2)设bn=2an,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练17练习卷(解析版) 题型:解答题
为了解某班学生喜爱打篮球是否与性别有关,对本班48人进行了问卷调查得到了如下的2×2列联表:
| 喜爱打篮球 | 不喜爱打篮球 | 合计 |
男生 |
| 6 |
|
女生 | 10 |
|
|
合计 |
|
| 48 |
已知在全班48人中随机抽取1人,抽到喜爱打篮球的学生的概率为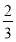 .
.
(1)请将上面的2×2列联表补充完整(不用写计算过程);
(2)你是否有95%的把握认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为X,求X的分布列与数学期望.
下面的临界值表供参考:
P(χ2≥x0)或 P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
x0(或k0) | 2.706 | 3.841 | 6.635 | 7.879 |
(参考公式)χ2=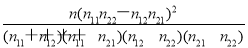 ,其中n=n11+n12+n21+n22或K2=
,其中n=n11+n12+n21+n22或K2=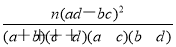 ,其中n=a+b+c+d)
,其中n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(解析版) 题型:选择题
过抛物线y2=2px(p>0)的焦点F且倾斜角为60°的直线l与抛物线分别交于A,B两点,则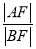 的值等于( ).
的值等于( ).
A.5 B.4 C.3 D.2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练15练习卷(解析版) 题型:解答题
设F1,F2分别是椭圆E:x2+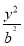 =1(0<b<1)的左、右焦点,过F1的直线l与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.
=1(0<b<1)的左、右焦点,过F1的直线l与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.
(1)求|AB|;
(2)若直线l的斜率为1,求b的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:解答题
在平面直角坐标系xOy中,曲线y=x2-6x+1与坐标轴的交点都在圆C上.
(1)求圆C的方程;
(2)若圆C与直线x-y+a=0交于A,B两点,且OA⊥OB,求a的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:选择题
已知圆(x-a)2+(y-b)2=r2的圆心为抛物线y2=4x的焦点,且与直线3x+4y+2=0相切,则该圆的方程为( ).
A.(x-1)2+y2=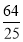 B.x2+(y-1)2=
B.x2+(y-1)2=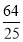
C.(x-1)2+y2=1 D.x2+(y-1)2=1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练12练习卷(解析版) 题型:填空题
如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC上一动点.现将△AFD沿AF折起,使平面ABD⊥平面ABC.在平面ABD内过点D作DK⊥AB,K为垂足.设AK=t,则t的取值范围是________.
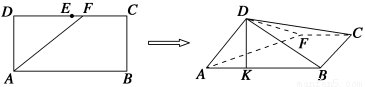
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷5练习卷(解析版) 题型:选择题
已知直线y=k(x-m)与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB于点D.若动点D的坐标满足方程x2+y2-4x=0,则m等于( ).
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com