
 设向量
设向量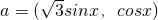 ,b=(cosx,cosx),记f(x)=a•b.
,b=(cosx,cosx),记f(x)=a•b.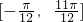 的简图,并指出该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到?
的简图,并指出该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到?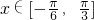 时,函数g(x)=f(x)+m的最小值为2,试求出函数g(x)的最大值并指出x取何值时,函数g(x)取得最大值.
时,函数g(x)=f(x)+m的最小值为2,试求出函数g(x)的最大值并指出x取何值时,函数g(x)取得最大值.


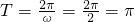 .
. | x | 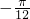 |  |  | 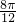 |  |
 | 0 |  | π |  | 2π |
sin( ) ) | 0 | 1 | 0 | -1 | 0 |
| y |  |  |  |  |  |

 单位得到函数
单位得到函数 的图象,再保持纵坐标不变,横坐标缩短为原为的
的图象,再保持纵坐标不变,横坐标缩短为原为的 得到函数
得到函数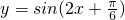 的图象,最后再向上平移
的图象,最后再向上平移 个单位得到就可得到函数
个单位得到就可得到函数 的图象.
的图象. 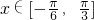 ,可得
,可得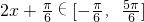 .
.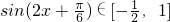 .
.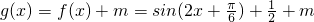 ,
,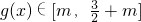 .
. .
.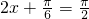 时,即
时,即 时,函数g(x)取得最大值
时,函数g(x)取得最大值 .
. ,进而求出函数的周期.
,进而求出函数的周期. 与x的范围,取值列表,描点,连线进而得到很多的图象.
与x的范围,取值列表,描点,连线进而得到很多的图象.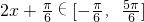 .所以
.所以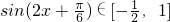 .所以
.所以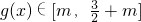 .结合题意求出m=2,,所以g(x)的最大值为
.结合题意求出m=2,,所以g(x)的最大值为 .并且此时
.并且此时 .
.

 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
| a |
| b |
| c |
| a |
| c |
| b |
| c |
| π |
| 3 |
| α-β |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| c |
| π |
| 6 |
| α-β |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| 3 |
| b |
| π |
| 3 |
| 2π |
| 3 |
| a |
| b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com