
定义一:对于一个函数 ,若存在两条距离为
,若存在两条距离为 的直线
的直线 和
和 ,使得
,使得 时,
时, 恒成立,则称函数
恒成立,则称函数 在
在 内有一个宽度为
内有一个宽度为 的通道.
的通道.
定义二:若一个函数 对于任意给定的正数
对于任意给定的正数 ,都存在一个实数
,都存在一个实数 ,使得函数
,使得函数 在
在 内有一个宽度为
内有一个宽度为 的通道,则称
的通道,则称 在正无穷处有永恒通道.
在正无穷处有永恒通道.
下列函数①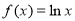 ;②
;②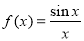 ;③
;③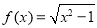 ;④
;④ ;⑤
;⑤ .其中在正无穷处有永恒通道的函数序号是 .
.其中在正无穷处有永恒通道的函数序号是 .
科目:高中数学 来源:2016届江西吉安一中高三三模考试数学(理)试卷(解析版) 题型:解答题
某工厂为了对新研发的产品进行合理定价,将该产品按实现拟定的价格进行试销,得到一组检测数据 (
(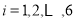 )如下表所示:
)如下表所示:
试销价格 | 4 | 5 | 6 | 7 |
| 9 |
产品销量 |
| 84 | 83 | 80 | 75 | 68 |
已知变量 具有线性负相关关系,且
具有线性负相关关系,且 ,
, ,现有甲、乙、丙三位同学通过计算求得其回归直线方程为:甲:
,现有甲、乙、丙三位同学通过计算求得其回归直线方程为:甲: ;乙:
;乙: ;丙:
;丙: ,其中有且仅有一位同学的计算是正确的.
,其中有且仅有一位同学的计算是正确的.
(1)试判断谁的计算结果是正确的?并求出 的值;
的值;
(2)若由线性回归方程得到的估计数据与检测数据的误差不超过1,则该检测数据是“理想数据”.现从检测数据中随机抽取3个,求“理想数据”个数 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川德阳香港马会五中高二下学期期中数学(理)试卷(解析版) 题型:选择题
执行如下图所示的程序框图,则输出的结果是

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2016届四川内江市高三第五次模拟考试数学(理)试卷(解析版) 题型:解答题
设非零向量 ,
, ,规定:
,规定: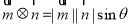 ,
,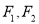 是椭圆
是椭圆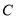 :
: 的左、右焦点,点
的左、右焦点,点 分别是其上顶点、右顶点,且
分别是其上顶点、右顶点,且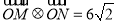 ,离心率
,离心率 .
.
(1)求椭圆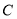 的方程;
的方程;
(2)过焦点 的直线交椭圆
的直线交椭圆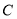 于点
于点 ,求
,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016届四川内江市高三第五次模拟考试数学(理)试卷(解析版) 题型:选择题
已知定义在 上的函数
上的函数 满足:
满足: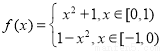 ,且
,且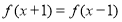 ,函数
,函数
 ,则方程
,则方程 在区间
在区间 上所有实根之和为
上所有实根之和为
A.-6 B.-8 C.-11 D.-12
查看答案和解析>>
科目:高中数学 来源:2016届四川内江市高三第五次模拟考试数学(理)试卷(解析版) 题型:选择题
下列说法正确的是
A.“ ”是“
”是“ ”的充分不必要条件
”的充分不必要条件
B.命题“ ”的否定是“
”的否定是“ ”
”
C.关于 的方程
的方程 的两实根异号的充要条件是
的两实根异号的充要条件是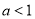
D.若 是
是 上的偶函数,则
上的偶函数,则 的图象的对称轴是
的图象的对称轴是 .
.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年长春第十一高中高二下学期期末数学理试卷(解析版) 题型:选择题
已知点 是抛物线
是抛物线 的焦点,点
的焦点,点 为抛物线
为抛物线 的对称轴与其准线的交点,过
的对称轴与其准线的交点,过 作抛物线
作抛物线 的切线,切点为
的切线,切点为 ,若点
,若点 恰好在以
恰好在以 为焦点的双曲线上,则双曲线的离心率为( )
为焦点的双曲线上,则双曲线的离心率为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届内蒙古赤峰市高三4月统一能力测试数学(理)试卷(解析版) 题型:解答题
某地区业余足球运动员共有15000人,其中男运动员9000人,女运动员6000人,为调查该地区业余足球运动员每周平均踢足球所占用时间的情况,采用分层抽样的方法,收集300位业余足球运动员每周平均踢足球所占用时间的样本数据(单位:小时),得到业余足球运动员每周平均踢足球所占用时间的频率分布直方图(如图所示),其中样本数据的分组区间为: .将“业余运动员的每周平均踢足球所占用时间超过4小时”定义为“热爱足球”.
.将“业余运动员的每周平均踢足球所占用时间超过4小时”定义为“热爱足球”.
(1)应收集多少位女运动员的样本数据?
(2)估计该地区每周平均踢足球所占用时间超过4小时的概率;
(3)在样本数据中,有80位女运动员“热爱足球”,请画出“热爱足球与性别”列联表,并判断是否有99%的把握认为“热爱足球与性别”有关.

附:
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com