
| |||||||||||||||
(1) |
解法一:∵正方形ABCD,∴CB⊥AB. ∵二面角C—AB—F是直二面角, CB⊥AB,∴CB⊥面ABEF. ∵AG,GB ∴CB⊥AG,CB⊥BG. 又AD=2a,AF=a,ABEF是矩形, G是EF的中点,
∴AG=BG= ∴AG⊥BG. ∵CB∩BG=B,∴AG⊥平面CBG, 而AG 如图,以A为原点建立直角坐标系, 则A(0,0,0),B(0,2a,0), C(0,2a,2a),G(a,a,0), F(a,0,0).
∴
∴AG=⊥BG,AG⊥BC,而BG与BC是平面BCG内两相交直线, ∴AG⊥平面BCG,又AG |
(2) |
解法一:如图,由(1)知面ACG⊥面BGC,且交于GC,在平面BGC内作BH⊥GC,垂足为H,则BH⊥平面AGC. ∴∠BGH是BG与平面AGC所成的角, ∴在Rt△CBG中 BH= 又BG= 解法二:设GB与平面AGC所成角为θ. 由题意可得 设平面AGC的一个法向量为n=(x,y,1), 由
(或:在证出 得cos< |
(3) |
解法一:由(2),BH⊥面AGC.作BO⊥AC,垂足为0,连结HO,则HO⊥AC, ∴∠BOH为二面角B—AC—G的平面角. ∵在Rt△ABC中,BO= ∴在Rt△BOH中, 即二面角B—AC—G的大小为arcsin 解法二:因n=(1,-1,1)是平面AGC的一个法向量, 又AF⊥平面ABCD,平面ABCD的一个法向量 ∴设n与 ∴二面角B—AC—G的大小为arccos |


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
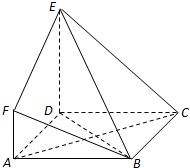 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,ABCD是边长为a的菱形,且∠BAD=60°,△PAD为正三角形,且面PAD⊥面ABCD.
如图,ABCD是边长为a的菱形,且∠BAD=60°,△PAD为正三角形,且面PAD⊥面ABCD.| AB |
| PD |
| EF |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,ABCD是边长为2的正方形,面EAD⊥面ABCD,且EA=ED,EF∥AB,且EF=1,O是线段AD的中点,三棱锥F-OBC的体积为
如图,ABCD是边长为2的正方形,面EAD⊥面ABCD,且EA=ED,EF∥AB,且EF=1,O是线段AD的中点,三棱锥F-OBC的体积为| 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•宁城县模拟)如图,ABCD是边长为1的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF.
(2012•宁城县模拟)如图,ABCD是边长为1的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B';折痕与AB交于点E,以EB和EB’为邻边作平行四边形EB’MB.若以B为原点,BC所在直线为x轴建立直角坐标系(如下图):
如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B';折痕与AB交于点E,以EB和EB’为邻边作平行四边形EB’MB.若以B为原点,BC所在直线为x轴建立直角坐标系(如下图):查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com