
【题目】在平面直角坐标系xOy中,圆C的参数方程为![]() (θ为参数),直线l经过点P(1,2),倾斜角α=
(θ为参数),直线l经过点P(1,2),倾斜角α=![]() .
.
(Ⅰ)写出圆C的标准方程和直线l的参数方程;
(Ⅱ)设直线l与圆C相交于A、B两点,求|PA||PB|的值.
科目:高中数学 来源: 题型:
【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水x(单位:千克)清洗该蔬菜1千克后,蔬菜上残留的农药y(单位:微克)的数据作了初步处理,得到下面的散点图及一些统计量的值.
y(微克)
 x(千克)
x(千克)
|
|
|
|
|
|
|
3 | 38 | 11 | 10 | 374 | -121 | -751 |
其中![]()
(I)根据散点图判断,![]() 与
与![]() ,哪一个适宜作为蔬菜农药残量
,哪一个适宜作为蔬菜农药残量![]() 与用水量
与用水量![]() 的回归方程类型(给出判断即可,不必说明理由);
的回归方程类型(给出判断即可,不必说明理由);
(Ⅱ)若用解析式![]()
![]() 与用水量
与用水量![]() 的回归方程,求出
的回归方程,求出![]() 与
与![]() 的回归方程.(c,d精确到0.1)
的回归方程.(c,d精确到0.1)
(Ⅲ)对于某种残留在蔬菜上的农药,当它的残留量低于20微克时对人体无害,为了放心食用该蔬菜,请估计需要用多少千克的清水清洗一千克蔬菜?(精确到0.1,参考数据![]() )
)
附:参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x),若在定义域内存在x0 , 使得f(﹣x0)=﹣f(x0)成立,则称x0为函数f(x)的局部对称点.
(1)若a,b,c∈R,证明函数f(x)=ax3+bx2+cx﹣b必有局部对称点;
(2)是否存在常数m,使得函数f(x)=4x﹣m2x+1+m2﹣3有局部对称点?若存在,求出m的范围,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() sin2x+sinxcosx.
sin2x+sinxcosx.
(Ⅰ)求函数f(x)的最小正周期和单调递增区间;
(Ⅱ)当x∈[0,![]() ]时,求函数f(x)的值域.
]时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0),e=
=1(a>b>0),e=![]() , 其中F是椭圆的右焦点,焦距为2,直线l与椭圆C交于点A、B,点A,B的中点横坐标为
, 其中F是椭圆的右焦点,焦距为2,直线l与椭圆C交于点A、B,点A,B的中点横坐标为![]() , 且
, 且![]() =λ
=λ![]() (其中λ>1).
(其中λ>1).
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)求实数λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列三图中的多边形均为正多边形,M,N是所在边的中点,双曲线均以图中的F1 , F2为焦点,设图示①②③中的双曲线的离心率分别为e1 , e2 , e3、则e1 , e2 , e3的大小关系为( )
A.e1>e2>e3
B.e1<e2<e3
C.e2=e3<e1
D.e1=e3>e2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足2Sn+an=1;递增的等差数列{bn}满足b1=1,b3=![]() ﹣4.
﹣4.
(1)求数列{an},{bn}的通项公式;
(2)若cn是an , bn的等比中项,求数列{![]() }的前n项和Tn;
}的前n项和Tn;
(3)若c![]() ≤
≤![]() t2+2t﹣2对一切正整数n恒成立,求实数t的取值范围.
t2+2t﹣2对一切正整数n恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知AD为圆O的直径,直线BA与圆O相切于点A,直线OB与弦AC垂直并相交于点G,与弧AC相交于M,连接DC,AB=10,AC=12.
(1)求证:BADC=GCAD;
(2)求BM.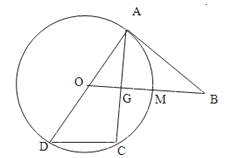
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角坐标系xOy中,曲线C的参数方程为 ![]() 为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为ρsin(θ+
为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为ρsin(θ+ ![]() )=2
)=2 ![]() .
.
(1)求曲线C在极坐标系中的方程;
(2)求直线l被曲线C截得的弦长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com