
 Ł©ŁŹ°ëŸ¶ÎȘ5ŁŹÖ±Ïß
Ł©ŁŹ°ëŸ¶ÎȘ5ŁŹÖ±Ïß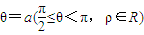 ±»ÔČœŰ”Ă”ÄÏÒł€ÎȘ8ŁŹÔòa= Łź
±»ÔČœŰ”Ă”ÄÏÒł€ÎȘ8ŁŹÔòa= Łź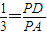 ŁŹÓÉPDĄÍAD żÉ”ĂŁŹcosĄÏAPD=
ŁŹÓÉPDĄÍAD żÉ”ĂŁŹcosĄÏAPD=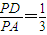 ŁŹÀûÓĂÍŹœÇÈęœÇșŻÊę”Ä»ù±ŸčŰÏ”Çó”ĂsinĄÏAPD”ÄÖ”Łź
ŁŹÀûÓĂÍŹœÇÈęœÇșŻÊę”Ä»ù±ŸčŰÏ”Çó”ĂsinĄÏAPD”ÄÖ”Łź ŒŽ y=tana•xŁŹtana•x-y=0Łź
ŒŽ y=tana•xŁŹtana•x-y=0Łź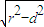 =2
=2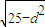 ŁŹĄàd=3ŁŹ
ŁŹĄàd=3ŁŹ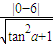 ŁŹĄàtana=±
ŁŹĄàtana=±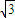 Łź
Łź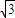 ŁŹa=
ŁŹa=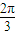 ŁŹčÊŽđ°žÎȘ
ŁŹčÊŽđ°žÎȘ  Łź
Łź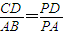 ŁŹ
ŁŹ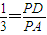 ŁźĄßPDĄÍADŁšÖ±Ÿ¶¶Ô”ÄÔČÖܜǔÈÓÚ90°Ł©ŁŹ
ŁźĄßPDĄÍADŁšÖ±Ÿ¶¶Ô”ÄÔČÖܜǔÈÓÚ90°Ł©ŁŹ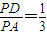 ŁŹĄàsinĄÏAPD=
ŁŹĄàsinĄÏAPD=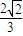 ŁŹčÊŽđ°žÎȘ
ŁŹčÊŽđ°žÎȘ 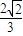 Łź
Łź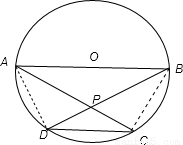



| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
 ŁšżŒÉúŚąÒâŁșÇëÔÚÏÂÁĐÈęÌâÖĐÈÎŃĄÒ»Ì⌜ŽđŁŹÈçčû¶àŚöŁŹÔò°ŽËùŚö”Ä”ÚÒ»ÌâÆÀ·ÖŁ©
ŁšżŒÉúŚąÒâŁșÇëÔÚÏÂÁĐÈęÌâÖĐÈÎŃĄÒ»Ì⌜ŽđŁŹÈçčû¶àŚöŁŹÔò°ŽËùŚö”Ä”ÚÒ»ÌâÆÀ·ÖŁ©
|
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
 ŁšÈęŃĄÒ»ŁŹżŒÉúŚąÒâŁșÇëÔÚÏÂÁĐÈęÌâÖĐÈÎŃĄÒ»Ì⌜ŽđŁŹÈçčû¶àŚöŁŹÔò°ŽËùŚö”Ä”ÚÒ»ÌâÆÀ·ÖŁ©
ŁšÈęŃĄÒ»ŁŹżŒÉúŚąÒâŁșÇëÔÚÏÂÁĐÈęÌâÖĐÈÎŃĄÒ»Ì⌜ŽđŁŹÈçčû¶àŚöŁŹÔò°ŽËùŚö”Ä”ÚÒ»ÌâÆÀ·ÖŁ©
|
| 3 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
 ŁšżŒÉúŚąÒâŁșÇëÔÚÏÂÁĐÈęÌâÖĐÈÎŃĄÒ»Ì⌜ŽđŁŹÈçčû¶àŚöŁŹÔò°ŽËùŚö”Ä”ÚÒ»ÌâÆÀÔÄŒÇ·ÖŁ©
ŁšżŒÉúŚąÒâŁșÇëÔÚÏÂÁĐÈęÌâÖĐÈÎŃĄÒ»Ì⌜ŽđŁŹÈçčû¶àŚöŁŹÔò°ŽËùŚö”Ä”ÚÒ»ÌâÆÀÔÄŒÇ·ÖŁ©| ŠĐ |
| 4 |
| 2 |
| 2 |
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
 ŁšżŒÉúŚąÒâŁșÇëÔÚÏÂÁĐÈęÌâÖĐÈÎŃĄÒ»Ì⌜ŽđŁŹÈçčû¶àŚöŁŹÔò°ŽËùŚö”Ä”ÚÒ»ÌâÆÀÔÄŒÇ·ÖŁ©
ŁšżŒÉúŚąÒâŁșÇëÔÚÏÂÁĐÈęÌâÖĐÈÎŃĄÒ»Ì⌜ŽđŁŹÈçčû¶àŚöŁŹÔò°ŽËùŚö”Ä”ÚÒ»ÌâÆÀÔÄŒÇ·ÖŁ©
|
|
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
|
| 4 |
| a |
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com