
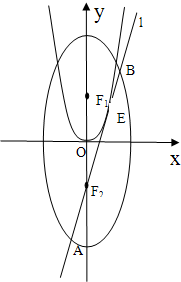
 ШчЭМЃЌвбжЊЭждВCЃК
ШчЭМЃЌвбжЊЭждВCЃК| x2 |
| b2 |
| y2 |
| a2 |
| F2B |
| AF2 |
| ET |
| EF1 |
| EF2 |
| 1 |
| 2 |
| ET |
| OT |
| 5 |
| 4 |
| x2 |
| b2 |
| y2 |
| a2 |
|
| ET |
| EF1 |
| EF2 |
| 1 |
| 2 |
|
| ET |
| OT |
| 5 |
| 4 |
| 5 |
| 5 |
|
| 5 |
2
| ||
| 2a2-5 |
| -(a2-5)2 |
| 2a2-5 |
| x2 |
| b2 |
| y2 |
| a2 |
| p |
| 2 |
|
|
| ET |
| EF1 |
| EF2 |
| 1 |
| 2 |
|
| ET |
| OT |
| 5 |
| 4 |
| ET |
| OT |
| t |
| 2 |
| ET |
| OT |
| t2 |
| 4 |
| 5 |
| 4 |
| 5 |
| p |
| 2 |
| p |
| 2 |
| 5 |
| 5 |
|
| 5 |
2
| ||
| 2a2-5 |
| -(a2-5)2 |
| 2a2-5 |
| F2B |
| AF2 |
2
| ||
| 2a2-5 |
| -(a2-5)2 |
| 2a2-5 |
| -(a2-5)2 |
| 2a2-5 |
| 20(a2-5)2 |
| (2a2-5)2 |
3
| ||
| 2 |
| ||||
|
| ||
| 3 |
2
| ||
| 2a2-5 |
| -(a2-5)2 |
| 2a2-5 |
| -(a2-5)2 |
| 2a2-5 |
| 1 |
| 9 |
| 20(a2-5)2 |
| (2a2-5)2 |
5
| ||
| 6 |
| ||||
|
3
| ||
| 5 |
| ||
| 3 |
3
| ||
| 5 |



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ШчЭМЃЌвбжЊЭждВCЃК
ШчЭМЃЌвбжЊЭждВCЃК| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 4 |
| x2 |
| 16 |
| y2 |
| 4 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ШчЭМЃЌвбжЊЭждВCЃК
ШчЭМЃЌвбжЊЭждВCЃК| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
| 2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ШчЭМЃЌвбжЊЭждВCЃК
ШчЭМЃЌвбжЊЭждВCЃК| x2 |
| 36 |
| y2 |
| 20 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ЃЈ2012•ЩюлквЛФЃЃЉШчЭМЃЌвбжЊЭждВCЃК
ЃЈ2012•ЩюлквЛФЃЃЉШчЭМЃЌвбжЊЭждВCЃК| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| TM |
| TN |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ШчЭМЃЌвбжЊЭждВCЃК
ШчЭМЃЌвбжЊЭждВCЃК| x2 |
| a2 |
| y2 |
| b2 |
| Іа |
| 4 |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com