
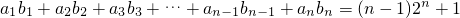 .
.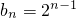 ,…(2分)
,…(2分)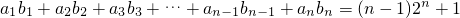 ,
,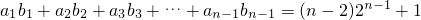 (n≥2),
(n≥2), ,即an=n.…(5分)
,即an=n.…(5分) ,∴
,∴ (n≥2)
(n≥2) …(11分)
…(11分)  是一个与n无关的常数,当且仅当a1=d≠0…(12分)
是一个与n无关的常数,当且仅当a1=d≠0…(12分) ;…(13分)
;…(13分) ,即
,即 (n≥2),若数列{bn}是等比数列,
(n≥2),若数列{bn}是等比数列, …(11分)
…(11分) ,…(13分)
,…(13分) 是一个与n无关的常数,当且仅当a1=d≠0,即可得到结论.
是一个与n无关的常数,当且仅当a1=d≠0,即可得到结论.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
| an | n |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com