
 等于( )
等于( )| A.恰有1只是坏的概率 | B.2只都是坏的概率 |
| C.2只全是好的概率 | D.至多1只是坏的概率 |
科目:高中数学 来源:不详 题型:解答题
 到
到 年十年间每年考入大学的人数.为方便计算,
年十年间每年考入大学的人数.为方便计算, 年编号为
年编号为 ,
, 年编号为
年编号为 ,…,
,…, 年编号为
年编号为 .数据如下:
.数据如下: 
 年中随机抽取两年,求考入大学人数至少有
年中随机抽取两年,求考入大学人数至少有 年多于
年多于 人的概率;
人的概率;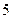 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出 关于
关于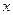 的回归方程
的回归方程 ,并计算第
,并计算第 年的估计值和实际值之间的差的绝对值.
年的估计值和实际值之间的差的绝对值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (总项目数足够多),现有3名工人独立地从中任选一个项目参与建设
(总项目数足够多),现有3名工人独立地从中任选一个项目参与建设 类别相同的概率;
类别相同的概率;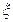 为3人中选择的项目属于B类工程或C类工程的人数,求
为3人中选择的项目属于B类工程或C类工程的人数,求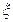 的分布列及数学期望.
的分布列及数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 .,每次命中与否互相独立.
.,每次命中与否互相独立.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下:
个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下:
 表示抽到“good sight”学生的人数,求
表示抽到“good sight”学生的人数,求 的分布列及数学期望.
的分布列及数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 动作 | K动作 | D动作 | ||
| 得分 | 100 | 80 | 40 | 10 |
| 概率 |  |  |  |  |
| 动作 | K动作 | D动作 | ||
| 得分 | 90 | 50 | 20 | 0 |
| 概率 |  |  |  |  |
 的分布列及数学期望
的分布列及数学期望
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com