
【题目】已知函数![]() 为
为![]() 的导函数.
的导函数.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 在
在![]() 上存在最大值0,求函数
上存在最大值0,求函数![]() 在[0,+∞)上的最大值.
在[0,+∞)上的最大值.
【答案】(1)见解析;(2)![]()
【解析】
(1)先求导,再分类讨论,即可求出g(x)的单调区间,(2)由(1)可知,a>0且 g(x)在 x=﹣lna处取得最大值,即![]() 构造函数 h(a)=a﹣lna﹣1(a>0),根据导数求出函数的最值,可知f(x)在[0,+∞)上单调递减,即可求解最大值
构造函数 h(a)=a﹣lna﹣1(a>0),根据导数求出函数的最值,可知f(x)在[0,+∞)上单调递减,即可求解最大值
(1)由题意可知,g(x)=f'(x)=x+a﹣aex,则g'(x)=1﹣aex,
当a≤0时,g'(x)>0,∴g(x)在(﹣∞,+∞)上单调递增;
当a>0时,解得x<﹣lna时,g'(x)>0,x>﹣lna时,g'(x)<0
∴g(x)在(﹣∞,﹣lna)上单调递增,在(﹣lna,+∞)上单调递减
综上,当a≤0时,g(x)的单调递增区间为(﹣∞,+∞),无递减区间;
当a>0时,g(x)的单调递增区间为 (﹣∞,﹣lna),单调递减区间为(﹣lna,+∞).
(2)由(1)可知,a>0且 g(x)在 x=﹣lna处取得最大值,
![]() ,即a﹣lna﹣1=0,
,即a﹣lna﹣1=0,
观察可得当a=1时,方程成立
令 h(a)=a﹣lna﹣1(a>0),![]()
当 a∈(0,1)时,h'(a)<0,当a∈(1,+∞)时,h'(a)>0
∴h(a)在(0,1)上单调递减,在 (1,+∞)单调递增,
∴h(a)≥h(1)=0,
∴当且仅当a=1时,a﹣lna﹣1=0,
∴![]() ,由题意可知 f'(x)=g(x)≤0,f(x)在[0,+∞)上单调递减,
,由题意可知 f'(x)=g(x)≤0,f(x)在[0,+∞)上单调递减,
∴f(x)在x=0处取得最大值f(0)=﹣1


科目:高中数学 来源: 题型:
【题目】2019年是新中国成立七十周年,新中国成立以来,我国文化事业得到了充分发展,尤其是党的十八大以来,文化事业发展更加迅速,下图是从2013 年到 2018 年六年间我国公共图书馆业机构数(个)与对应年份编号的散点图(为便于计算,将 2013 年编号为 1,2014 年编号为 2,…,2018年编号为 6,把每年的公共图书馆业机构个数作为因变量,把年份编号从 1 到 6 作为自变量进行回归分析),得到回归直线![]() ,其相关指数
,其相关指数![]() ,给出下列结论,其中正确的个数是( )
,给出下列结论,其中正确的个数是( )

①公共图书馆业机构数与年份的正相关性较强
②公共图书馆业机构数平均每年增加13.743个
③可预测 2019 年公共图书馆业机构数约为3192个
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直角梯形![]() 与等腰直角三角形
与等腰直角三角形![]() 所在的平面互相垂直.
所在的平面互相垂直.![]()
![]() ,
,![]() ,
,![]() .
.
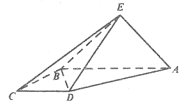
(1)求证:![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,∠C=![]() ,AC=BC,M、N分别是BC、AB的中点,将△BMN沿直线MN折起,使二面角B′﹣MN﹣B的大小为
,AC=BC,M、N分别是BC、AB的中点,将△BMN沿直线MN折起,使二面角B′﹣MN﹣B的大小为![]() ,则B'N与平面ABC所成角的正切值是( )
,则B'N与平面ABC所成角的正切值是( )
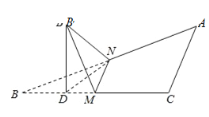
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】勒洛三角形是具有类似圆的“定宽性”的面积最小的曲线,它由德国机械工程专家,机构运动学家勒洛首先发现,其作法是:以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形就是勒洛三角形,现在勒洛三角形中随机取一点,则此点取自正三角形外的概率为( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 与
与![]() 的图象上存在关于原点对称的点,求实数
的图象上存在关于原点对称的点,求实数![]() 的取值范围;
的取值范围;
(2)设![]() ,已知
,已知![]() 在
在![]() 上存在两个极值点
上存在两个极值点![]() ,且
,且![]() ,求证:
,求证:![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com