
【题目】已知函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,即
,即![]() ,若
,若![]() ,则称
,则称![]() 在
在![]() 上封闭.
上封闭.
(1)分别判断函数![]() ,
, ![]() 在
在![]() 上是否封闭,说明理由;
上是否封闭,说明理由;
(2)函数![]() 的定义域为
的定义域为![]() ,且存在反函数
,且存在反函数![]() ,若函数
,若函数![]() 在
在![]() 上封闭,且函数
上封闭,且函数![]() 在
在![]() 上也封闭,求实数
上也封闭,求实数![]() 的取值范围;
的取值范围;
(3)已知函数![]() 的定义域为
的定义域为![]() ,对任意
,对任意![]() ,若
,若![]() ,有
,有![]() 恒成立,则称
恒成立,则称![]() 在
在![]() 上是单射,已知函数
上是单射,已知函数![]() 在
在![]() 上封闭且单射,并且满足
上封闭且单射,并且满足![]()
![]() ,其中
,其中![]() (
(![]() ),
),![]() ,证明:存在
,证明:存在![]() 的真子集,
的真子集, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,使得
,使得![]() 在所有
在所有![]() (
(![]() )上封闭.
)上封闭.
【答案】(1)见解析;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:(1)根据![]() 在
在![]() 上封闭的定义,分别求出函数
上封闭的定义,分别求出函数![]() ,
, ![]() 在
在![]() 上的值域,即可判断是否封闭;(2)函数
上的值域,即可判断是否封闭;(2)函数![]() 在D上封闭,则
在D上封闭,则![]() .函数
.函数![]() 在
在![]() 上封闭,则
上封闭,则![]() ,得到:
,得到: ![]() .从而问题转化为:
.从而问题转化为: ![]() 在
在![]() 两不等实根.(3)分两种情况:
两不等实根.(3)分两种情况: ![]() 和
和![]() ,第一种情况显然不成立,第二种情况,因为
,第一种情况显然不成立,第二种情况,因为![]() 是单射,因此取一个
是单射,因此取一个![]() ,则
,则![]() 是唯一的使得
是唯一的使得![]() 的根,换句话说
的根,换句话说![]() 考虑到
考虑到![]() ,即
,即![]() ,因为
,因为![]() 是单射,则
是单射,则![]() 这样就有了
这样就有了![]() .接着令
.接着令![]() ,并重复上述论证证明
,并重复上述论证证明![]() ..
..
试题解析:
(1)因为函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,(取一个具体例子也可),
,(取一个具体例子也可),
所以![]() 在
在![]() 上不封闭.
上不封闭.
![]()
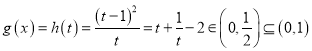
![]() 在
在![]() 上封闭
上封闭
(2)函数![]() 在D上封闭,则
在D上封闭,则![]() .函数
.函数![]() 在
在![]() 上封闭,则
上封闭,则![]() ,
,
得到: ![]() .
.
![]() 在
在![]() 单调递增.
单调递增.
则![]()
![]() 在
在![]() 两不等实根.
两不等实根.
![]() ,
,
故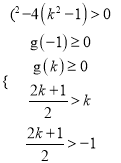 ,解得
,解得![]() .
.
另解: ![]() 在
在![]() 两不等实根.令
两不等实根.令![]()
![]() 在
在![]() 有两个不等根,画图,由数形结合可知,
有两个不等根,画图,由数形结合可知, ![]()
解得![]() .
.
(3)如果![]() ,则
,则![]() ,与题干
,与题干![]() 矛盾.
矛盾.
因此![]() ,取
,取![]() ,则
,则![]() .
.
接下来证明![]() ,因为
,因为![]() 是单射,因此取一个
是单射,因此取一个![]() ,
,
则![]() 是唯一的使得
是唯一的使得![]() 的根,换句话说
的根,换句话说![]()
考虑到![]() ,即
,即![]() ,
,
因为![]() 是单射,则
是单射,则![]()
这样就有了![]() .
.
接着令![]() ,并重复上述论证证明
,并重复上述论证证明![]() ..
..


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】随着我国经济的快速发展,民用汽车的保有量也迅速增长.机动车保有量的发展影响到环境质量、交通安全、道路建设等诸多方面.在我国,尤其是大中型城市,机动车已成为城市空气污染的重要来源.因此,合理预测机动车保有量是未来进行机动车污染防治规划、道路发展规划等的重要前提.从2012年到2016年,根据“云南省某市国民经济和社会发展统计公报”中公布的数据,该市机动车保有量数据如表所示.
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
机动车保有量 | 169 | 181 | 196 | 215 | 230 |
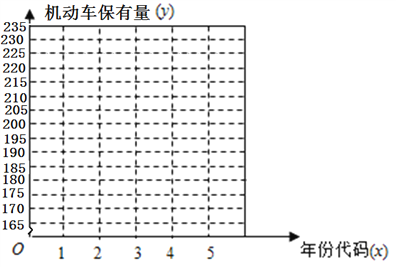
(1)在图所给的坐标系中作出数据对应的散点图;
(2)建立机动车保有量![]() 关于年份代码
关于年份代码![]() 的回归方程;
的回归方程;
(3)按照当前的变化趋势,预测2017年该市机动车保有量.
附注:回归直线方程![]() 中的斜率和截距的最小二乘估计公式分别为:
中的斜率和截距的最小二乘估计公式分别为:
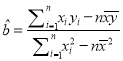 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
, ![]() ,
, ![]() ,
, ![]() 满足
满足![]() ,且当
,且当![]() 时,
时, ![]() ,令
,令![]() .
.
(Ⅰ)写出![]() 的所有可能的值.
的所有可能的值.
(Ⅱ)求![]() 的最大值.
的最大值.
(Ⅲ)是否存在数列![]() ,使得
,使得![]() ?若存在,求出数列
?若存在,求出数列![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知定圆![]() ,定直线
,定直线![]() ,过
,过![]() 的一条动直线
的一条动直线![]() 与直线相交于
与直线相交于![]() ,与圆
,与圆![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 是
是![]() 中点.
中点.
(Ⅰ)当![]() 与
与![]() 垂直时,求证:
垂直时,求证:![]() 过圆心
过圆心![]() ;
;
(Ⅱ)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(Ⅲ)设![]() ,试问
,试问![]() 是否为定值,若为定值,请求出
是否为定值,若为定值,请求出![]() 的值;若不为定值,请说明理由.
的值;若不为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,M,N分别为
中,M,N分别为![]() 的中点.
的中点.
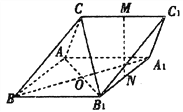
(1)证明:直线MN//平面CAB1;
(2)若四边形ABB1A1是菱形,且![]() ,
, ![]() ,求平面
,求平面![]() 和平面
和平面![]() 所成的角(锐角)的余弦值.
所成的角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
极坐标系的极点为直角坐标系![]() 的原点,极轴为
的原点,极轴为![]() 轴的正半轴,两神坐标系中的长度单位相同.已知曲线
轴的正半轴,两神坐标系中的长度单位相同.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)在曲线![]() 上求一点,使它到直线
上求一点,使它到直线![]() :
:  (
(![]() 为参数)的距离最短,写出
为参数)的距离最短,写出![]() 点的直角坐标.
点的直角坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com