
 满足
满足 ,
, .
. 的通项公式;
的通项公式; ,数列{bn}的前n项和为Tn,试比较Tn与
,数列{bn}的前n项和为Tn,试比较Tn与 的大小,并予以证明.
的大小,并予以证明. ;(2)详见解析.
;(2)详见解析. 的递推式的结构为
的递推式的结构为 ,在求数列的通项的时候可以利用累加法来求数列
,在求数列的通项的时候可以利用累加法来求数列 的通项公式;(2)先求出数列
的通项公式;(2)先求出数列 的通项公式,根据其通项结构选择错位相减法求出数列
的通项公式,根据其通项结构选择错位相减法求出数列 的前
的前 项和
项和 ,在比较
,在比较 与
与 的大小时,一般利用作差法,通过差的正负确定
的大小时,一般利用作差法,通过差的正负确定 与
与 的大小,在确定差的正负时,可以利用数学归纳法结合二项式定理进行放缩来达到证明不等式的目的.
的大小,在确定差的正负时,可以利用数学归纳法结合二项式定理进行放缩来达到证明不等式的目的. 时,
时,


 .
. 也适合上式,所以
也适合上式,所以 .
. ,所以
,所以 .
.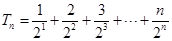 ①,所以
①,所以 ②.
②. ,
, .
. ,
, 与
与 的大小关系等价于比较
的大小关系等价于比较 与
与 的大小.
的大小. 时,
时, ;当
;当 时,
时, ;
; 时,
时, ;当
;当 时,
时, ;……,
;……, 时,
时, .
. 时,
时,
 .
. 或
或 时,
时, ;当
;当 时,
时, .
.

科目:高中数学 来源:不详 题型:解答题
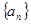 的前n项和为
的前n项和为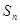 ,
,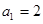 ,当n≥2时,
,当n≥2时,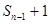 ,
,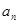 ,
,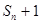 成等差数列. (1)求数列
成等差数列. (1)求数列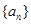 的通项公式;
的通项公式;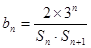 ,
,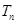 是数列
是数列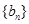 的前n项和,求使得
的前n项和,求使得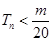 对所有
对所有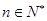 都成立的最小正整数
都成立的最小正整数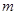 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com