
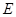 中,已知
中,已知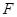 ,
,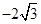 ,
,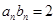 (
(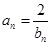 ,
,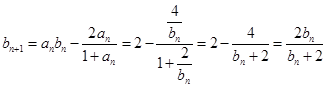 ).
).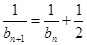 ,
,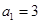 时,分别求
时,分别求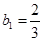 的值,判断
的值,判断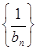 是否为定值,并给出证明;
是否为定值,并给出证明;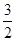 ,使得
,使得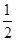 为完全平方数.
为完全平方数.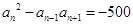 (
(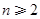 ).(2)当
).(2)当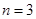 时,满足条件.
时,满足条件.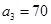 ,
,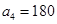 .所以
.所以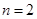 时,
时,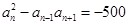 ;当
;当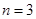 时,
时,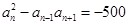 .第二步猜想,
.第二步猜想,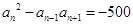 (
(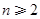 ).第三步证明,本题可用数学归纳法证,也可证等式
).第三步证明,本题可用数学归纳法证,也可证等式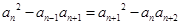 恒成立,(2)探求整数解问题,一般要构造一个可说明的整式. 设
恒成立,(2)探求整数解问题,一般要构造一个可说明的整式. 设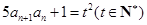 ,则
,则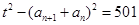 ,又
,又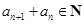 ,且501=1
,且501=1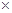 501=3
501=3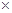 167,故
167,故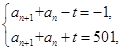 或
或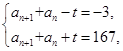 所以
所以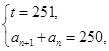 或
或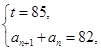
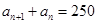 解得
解得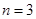 ;由
;由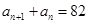 得
得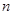 无整数解.所以当
无整数解.所以当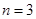 时,满足条件.
时,满足条件.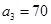 ,
,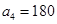 .
.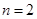 时,
时,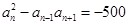 ;当
;当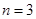 时,
时,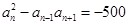 . 2分
. 2分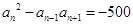 (
(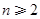 ). 3分
). 3分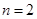 时,结论成立.
时,结论成立.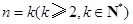 时,结论成立,即
时,结论成立,即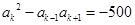 ,
,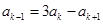 代入上式,可得
代入上式,可得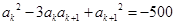 .
.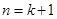 时,
时,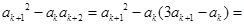
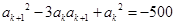 .
.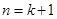 结论成立,
结论成立,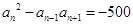 (
(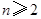 )成立. 5分
)成立. 5分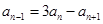 代入
代入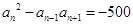 ,得
,得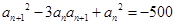 ,
,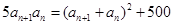 ,
,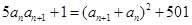 ,
,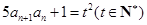 ,则
,则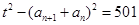 ,
,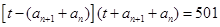 , 7分
, 7分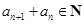 ,且501=1
,且501=1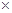 501=3
501=3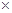 167,
167,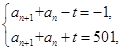 或
或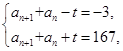
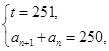 或
或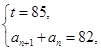
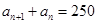 解得
解得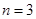 ;由
;由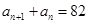 得
得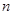 无整数解.
无整数解.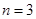 时,满足条件. 10分
时,满足条件. 10分

科目:高中数学 来源:不详 题型:填空题
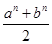 ≥
≥ n(a,b是非负实数,n∈N+)时,假设n
n(a,b是非负实数,n∈N+)时,假设n查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
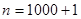 时它也成立,下列判断中,正确的是( )
时它也成立,下列判断中,正确的是( )| A.P(k)对k=2013成立 | B.P(k)对每一个自然数k成立 |
| C.P(k)对每一个正偶数k成立 | D.P(k)对某些偶数可能不成立 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com