
【题目】在棱长为1的正方体![]() 中,E,F分别为线段CD和
中,E,F分别为线段CD和![]() 上的动点,且满足
上的动点,且满足![]() ,则四边形
,则四边形![]() 所围成的图形(如图所示阴影部分)分别在该正方体有公共顶点的三个面上的正投影的面积之和( )
所围成的图形(如图所示阴影部分)分别在该正方体有公共顶点的三个面上的正投影的面积之和( )

A. 有最小值![]() B. 有最大值
B. 有最大值![]() C. 为定值3D. 为定值2
C. 为定值3D. 为定值2
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣2x﹣3≤0},B={x|x2﹣2mx+m2﹣4≤0,x∈R,m∈R}.
(1)若A∪B=A,求实数m的取值;
(2)若A∩B={x|0≤x≤3},求实数m的值;
(3)若A![]() ,求实数m的取值范围.
,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车已成为一种时髦的新型环保交通工具,某共享单车公司为了拓展市场,对![]() 两个品牌的共享单车在编号分别为
两个品牌的共享单车在编号分别为![]() 的五个城市的用户人数(单位:十万)进行统计,得到数据如下:
的五个城市的用户人数(单位:十万)进行统计,得到数据如下:
城市 品牌 | 1 | 2 | 3 | 4 | 5 |
A品牌 | 3 | 4 | 12 | 6 | 8 |
B品牌 | 4 | 3 | 7 | 9 | 5 |
(Ⅰ)若共享单车用户人数超过50万的城市称为“优城”,否则称为“非优城”,据此判断能否有85%的把握认为“优城”和共享单车品牌有关?
(Ⅱ)若不考虑其它因素,为了拓展市场,对A品牌要从这五个城市选择三个城市进行宣传,
(ⅰ)求城市2被选中的概率;
(ⅱ)求在城市2被选中的条件下城市3也被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下给出了4个命题:
(1)两个长度相等的向量一定相等;
(2)相等的向量起点必相同;
(3)若![]() ,且
,且![]() ,则
,则![]() ;
;
(4)若向量![]() 的模小于
的模小于![]() 的模,则
的模,则![]() .
.
其中正确命题的个数共有( )
A.3 个B.2 个C.1 个D.0个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知一动圆经过点
中,已知一动圆经过点![]() 且在
且在![]() 轴上截得的弦长为4,设动圆圆心的轨迹为曲线
轴上截得的弦长为4,设动圆圆心的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() ,
,![]() ,
,![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点
两点![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,线段
两点,线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() ,求证:直线
,求证:直线![]() 过定点
过定点![]() ,并求出定点
,并求出定点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 的图像与
的图像与![]() 轴无交点,求
轴无交点,求![]() 的取值范围;
的取值范围;
(2)若方程![]() 在区间
在区间![]() 上存在实根,求
上存在实根,求![]() 的取值范围;
的取值范围;
(3)设函数![]() ,
,![]() ,当
,当![]() 时若对任意的
时若对任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为F,过点F作垂直于x轴的直线与抛物线交于A,B两点,且以线段AB为直径的圆过点
的焦点为F,过点F作垂直于x轴的直线与抛物线交于A,B两点,且以线段AB为直径的圆过点![]() .
.
(1)求抛物线C的方程;
(2)设过点![]() 的直线
的直线![]() 分别与抛物线C交于点D,E和点G,H,且
分别与抛物线C交于点D,E和点G,H,且![]() ,求四边形
,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某学校的特长班有50名学生,其中有体育生20名,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75],按上述分组方法得到的频率分布直方图如图所示.因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若前两组的学生中体育生有8名.
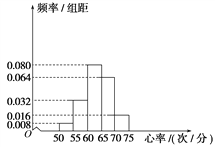
(1)根据频率分布直方图及题设数据完成下列2×2列联表.
心率小于60次/分 | 心率不小于60次/分 | 合计 | |
体育生 | 20 | ||
艺术生 | 30 | ||
合计50 |
(2)根据(1)中表格数据计算可知,________(填“有”或“没有”)99.5%的把握认为“心率小于60次/分与常年进行系统的身体锻炼有关”.
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com