|
|
|
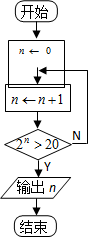
下图是一个算法流程图,则输出的 n的值是________.
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:苏教版(新课标) 必修1
题型:
|
|
|
某工厂经奥组委授权生产销售伦敦奥运会吉祥物(精灵”文洛克”)饰品,生产该饰品的全部成本c与生产的饰品的件数x(单位:万件)满足函数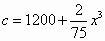 (单位:万元);该饰品单价p(单位:元)的平方与生产的饰品件数x(单位:万件)成反比,现已知生产该饰品100万件时,其单价p=50元.且工厂生产的饰品都可以销售完.设工厂生产该饰品的利润为f(x)(万元)(注:利润=销售额-成本) (单位:万元);该饰品单价p(单位:元)的平方与生产的饰品件数x(单位:万件)成反比,现已知生产该饰品100万件时,其单价p=50元.且工厂生产的饰品都可以销售完.设工厂生产该饰品的利润为f(x)(万元)(注:利润=销售额-成本)
(Ⅰ)求函数y=f(x)的表达式.
(Ⅱ)当生产该饰品的件数x(万件)为多少时,工厂生产该饰品的利润最大.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
甲乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛,假设每局甲获胜的概率为,乙获胜的概率为,各局比赛结果相互独立.
(1)求甲在4局以内(含4局)赢得比赛的概率;
(2)记为比赛决出胜负时的总局数,求的分布列和均值(数学期望).
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
(x-2)6的展开式中x3的系数为________.(用数字作答)
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别是0.6,0.5,0.5,0.4,各人是否使用设备相互独立,
(1)求同一工作日至少3人需使用设备的概率;
(2)实验室计划购买k台设备供甲、乙、丙、丁使用,若要求“同一工作日需使用设备的人数大于k”的概率小于0.1,求k的最小值.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设甲、乙两个圆柱的底面积分别为 S1,S2,体积分别为V1,V2,若它们的侧面积相等,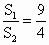 ,则 ,则 ________. ________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
在平面直角坐标系中,曲线C: (t为参数)的普通方程为________. (t为参数)的普通方程为________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:置如其周,令相乘也.又以高乘之,三十六成一.该术相当于给出了由圆锥的底面周长L与高h,计算其体积V的近似公式V≈ L2h.它实际上是将圆锥体积公式中的圆周率π近似取为3.那么,近似公式V≈ L2h.它实际上是将圆锥体积公式中的圆周率π近似取为3.那么,近似公式V≈ L2h相当于将圆锥体积公式中的π近似取为 L2h相当于将圆锥体积公式中的π近似取为
|
| [ ] |
A. |
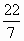
|
B. |
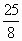
|
C. |
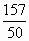
|
D. |
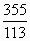
|
|
|
查看答案和解析>>

 初中暑期衔接系列答案
初中暑期衔接系列答案