
设数列{an}满足:a1=1,a2=2,an+2=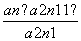 (n≥1,n∈N*),
(n≥1,n∈N*),
令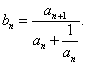
(1) 求证:数列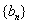 是常数列;
是常数列;
(2) 求证:当n≥2时,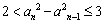 ;
;
(3) 求a2 015的整数部分.
(1) 易知,对一切n≥1,an≠0,由an+2=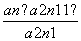 ,得
,得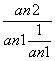 =
=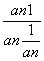 .
.
依次利用上述关系式,可得
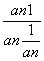 =
=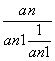 =
=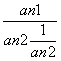 =…=
=…= =
=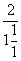 =1,
=1,
从而数列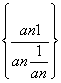 是常数列.
是常数列.
(2) 由(1)得an+1=an+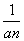 .
.
又a1=1,∴可知数列{an}递增,则对一切n≥1,有an≥1成立,从而0<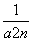 ≤1.
≤1.
当n≥2时,a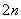 =
=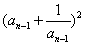 =a
=a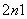 +
+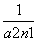 +2,
+2,
于是a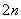 -a
-a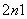 =
=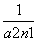 +2,
+2,
∴2<a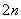 -a
-a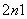 ≤3.
≤3.
(3) 当n≥2时,a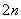 =a
=a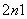 +
+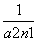 +2,
+2,
∴a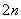 =
=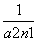 +…+
+…+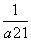 +a
+a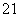 +2(n-1).
+2(n-1).
a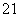 =1,a
=1,a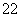 =4,则当n≥3时,
=4,则当n≥3时,
a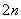 =
=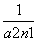 +…+
+…+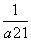 +a
+a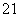 +2(n-1)
+2(n-1)
=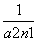 +…+
+…+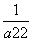 +1+1+2(n-1)
+1+1+2(n-1)
=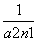 +…+
+…+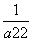 +2n>2n.
+2n>2n.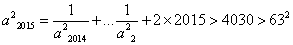 ,
,
又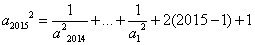
=4 029+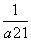 +…+
+…+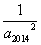 =4 030+
=4 030+
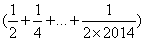
=4 030+
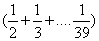 +
+
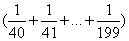 +
+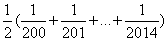
<4 030+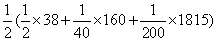 <4 096=642.
<4 096=642.
∴63<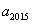 <64,即
<64,即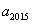 的整数部分为63.
的整数部分为63.


 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:
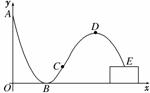
轮滑是穿着带滚轮的特制鞋在坚硬的场地上滑行的运动.如图,助跑道ABC是一段抛物线,某轮滑运动员通过助跑道获取速度后飞离跑道然后落到离地面高为1 m的平台上E处,飞行的轨迹是一段抛物线CDE(抛物线CDE与抛物线ABC在同一平面内),D为这段抛物线的最高点.现在运动员的滑行轮迹所在平面上建立如图所示的直角坐标系,x轴在地面上,助跑道一端点A(0,4),另一端点C(3,1),点B(2,0),单位:m.
(1)求助跑道所在的抛物线方程;
(2)若助跑道所在抛物线与飞行轨迹所在抛物线在点C处有相同的切线,为使运动员安全和空中姿态优美,要求运动员的飞行距离在4 m到6 m之间(包括4 m和6 m),试求运动员飞行过程中距离平台最大高度的取值范围.
(注:飞行距离指点C与点E的水平距离,即这两点横坐标差的绝对值)
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE=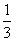 BB1,C1F=
BB1,C1F=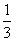 CC1.
CC1.
(1)求异面直线AE与A1 F所成角的大小;
(2)求平面AEF与平面ABC所成角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
下列说法中,正确的个数是( )
(1)在频率分布直方图中,中位数左边和右边的直方图的面积相等.
(2)如果一组数中每个数减去同一个非零常数,则这一组数的平均数改变,方差不改变.
(3)对于命题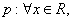
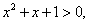 则
则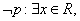
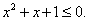 .
.
(4)命题“在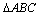 中,若
中,若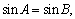 则
则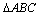 为等腰三角形”的否命题为真命题.
为等腰三角形”的否命题为真命题.
A. 4 B. 3 C .2 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
以直角坐标系的原点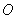 为极点,
为极点, 轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线
轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线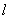 的参数方程为
的参数方程为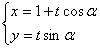 (
(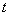 为参数,
为参数,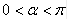 ),曲线
),曲线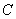 的极坐标方程为
的极坐标方程为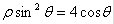 .
.
(Ⅰ)求曲线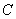 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线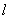 与曲线
与曲线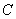 相交于
相交于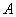 、
、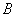 两点,当
两点,当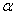 变化时,求
变化时,求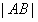 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com