
已知点N(1,2),过点N的直线交双曲线x2-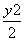 =1于A,B两点,且
=1于A,B两点,且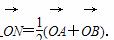
(1)求直线AB的方程;
(2)若过N的另一条直线交双曲线于C,D两点,且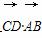 =0,那么A,B,C,D四点是否共圆?为什么?
=0,那么A,B,C,D四点是否共圆?为什么?
(1)由题意知直线AB的斜率存在.
设直线AB:y=k(x-1)+2,代入x2-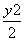 =1得,
=1得,
(2-k2)x2-2k·(2-k)x-(2-k)2-2=0.(*)
设A(x1,y1),B(x2,y2),则x1,x2是方程(*)的两根,
∴2-k2≠0且x1+x2=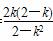 .
.
∵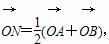 ,∴N是AB的中点,∴
,∴N是AB的中点,∴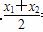 =1,
=1,
∴k(2-k)=-k2+2,∴k=1,
∴AB的方程为y=x+1.
(2)将k=1代入方程(*)得x2-2x-3=0,
∴x=-1或x=3,
不妨设A(-1,0),B(3,4).
∵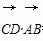 =0,∴CD垂直平分AB.
=0,∴CD垂直平分AB.
∴CD所在直线方程为y=-(x-1)+2,即y=3-x,
代入双曲线方程整理得x2+6x-11=0,
令C(x3,y3),D(x4,y4)及CD中点M(x0,y0),
则x3+x4=-6,x3·x4=-11,
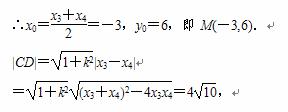 |MC|=|MD|=
|MC|=|MD|=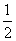 |CD|=2
|CD|=2 ,
,
|MA|=|MB|=2 ,
,
即A,B,C,D到M的距离相等,∴A,B,C,D四点共圆.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
若原点O和点F(-2,0)分别为双曲线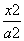 -y2=1(a>0)的中心和左焦点,点P为双曲线右支上的任意一点,则
-y2=1(a>0)的中心和左焦点,点P为双曲线右支上的任意一点,则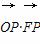 的取值范围为( )
的取值范围为( )
A.[3-2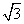 ,+∞) B.[3+2
,+∞) B.[3+2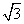 ,+∞)
,+∞)
C.[-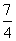 ,+∞) D.[
,+∞) D.[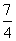 ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
设M(x0,y0)为抛物线C:x2=8y上一点,F为抛物线C的焦点,以F为圆心、|FM|为半径的圆和抛物线C的准线相交,则y0的取值范围是( )
A.(0,2) B.[0,2]
C.(2,+∞) D.[2,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com