
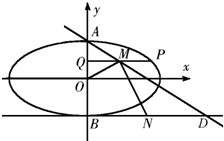
 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,A,B分别是C的上下顶点,点B在直线l:y=-1上.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,A,B分别是C的上下顶点,点B在直线l:y=-1上.分析 (Ⅰ)根据椭圆的定义与几何性质,求出a、b的值即可;
(Ⅱ)设出点P的坐标,得出Q、M与N的坐标,表示出$\overrightarrow{MN}$、$\overrightarrow{OM}$,利用平面向量的数量积判断$\overrightarrow{MN}$⊥$\overrightarrow{OM}$即可.
解答 解:(Ⅰ)依题意,得$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,b=1,
因为a2-c2=b2,
所以a2=4,
故椭圆C的方程为$\frac{{x}^{2}}{4}$+y2=1;…(4分)
(Ⅱ)设P(x0,y0)(x0≠0),则Q(0,y0),
$\frac{{{x}_{0}}^{2}}{4}$+${{y}_{0}}^{2}$=1;
因为M为线段PQ的中点,所以M($\frac{{x}_{0}}{2}$,y0),
又A(0,1),所以直线AM的方程为y=$\frac{2{(y}_{0}-1)}{{x}_{0}}$x+1,
令y=-1,得D($\frac{{x}_{0}}{1{-y}_{0}}$,-1),
又B(0,-1),N为线段BD的中点,所以N($\frac{{x}_{0}}{2(1{-y}_{0})}$,-1),
所以$\overrightarrow{MN}$=($\frac{{x}_{0}}{2(1{-y}_{0})}$-$\frac{{x}_{0}}{2}$,-1-y0),
所以$\overrightarrow{MN}$•$\overrightarrow{OM}$=$\frac{{x}_{0}}{2}$($\frac{{x}_{0}}{2(1{-y}_{0})}$-$\frac{{x}_{0}}{2}$)+y0(-1-y0)
=$\frac{{{x}_{0}}^{2}}{4}$•$\frac{1}{1{-y}_{0}}$-y0-($\frac{{{x}_{0}}^{2}}{4}$+${{y}_{0}}^{2}$)
=(1-${{y}_{0}}^{2}$)•$\frac{1}{1{-y}_{0}}$-y0-1
=0,
所以$\overrightarrow{MN}$⊥$\overrightarrow{OM}$,
即MN⊥OM.…(12分)
点评 本题考查了平面向量的应用问题,也考查了椭圆的定义与几何性质的应用问题,考查了直线与椭圆的综合应用问题,是综合性题目.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:解答题
 已知点p(c,$\frac{3}{2}$c)在以F(c,0)为右焦点的椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,斜率为1的直线m过点F与椭圆Γ交于A,B两点,且与直线l:x=4c交于点M.
已知点p(c,$\frac{3}{2}$c)在以F(c,0)为右焦点的椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,斜率为1的直线m过点F与椭圆Γ交于A,B两点,且与直线l:x=4c交于点M.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2035 | B. | 2036 | C. | 4084 | D. | 4085 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}≤θ≤\frac{π}{2}$ | B. | $\frac{π}{3}≤θ≤\frac{π}{2}$ | C. | $0≤θ≤\frac{π}{3}$ | D. | $0<θ<\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
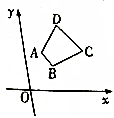 已知梯形ABCD,如图所示,其中AB∥CD,且DC=2AB,三个顶点的坐标分别为A(1,2)、B(2,1)、C(4,2),求点D的坐标.
已知梯形ABCD,如图所示,其中AB∥CD,且DC=2AB,三个顶点的坐标分别为A(1,2)、B(2,1)、C(4,2),求点D的坐标.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 26 | C. | 29 | D. | 212 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 720 | B. | 270 | C. | 390 | D. | 300 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com