
| A. | 2035 | B. | 2036 | C. | 4084 | D. | 4085 |
分析 先利用换底公式与叠乘法把a1•a2•a3•…•ak化为log2(k+1),然后根据a1•a2•a3•…•ak为整数可得k=2n-1,最后由等比数列前n项和公式解决问题.
解答 解:∵an=logn(n+1)=$\frac{lo{g}_{2}(n+1)}{lo{g}_{2}n}$,(n≥2,n∈N*),
∴a1•a2•a3•…•ak=$\frac{lo{g}_{2}3}{lo{g}_{2}2}$×$\frac{lo{g}_{2}4}{lo{g}_{2}3}$×…×$\frac{lo{g}_{2}(k+1)}{lo{g}_{2}k}$=log2(k+1),
又∵a1•a2•a3•…•ak为整数,
∴k+1必须是2的n次幂(n∈N*),即k=2n-1.
∴k∈[1,2015]内所有的“幸运数”的和
M=(22-1)+(23-1)+(24-1)+…+(210-1)
=$\frac{4(1-{2}^{9})}{1-2}$-1×9
=2035,
故选:A.
点评 本题在理解新定义的基础上,考查换底公式、叠乘法及等比数列前n项和公式,其综合性、技巧性较强,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别是F1(-c,0),F2(c,0),直线l:x=my-c与椭圆C交于点M,N两点,当m=-$\frac{{\sqrt{3}}}{3}$,M是椭圆C的顶点,且△MF1F2的周长为6.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别是F1(-c,0),F2(c,0),直线l:x=my-c与椭圆C交于点M,N两点,当m=-$\frac{{\sqrt{3}}}{3}$,M是椭圆C的顶点,且△MF1F2的周长为6.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
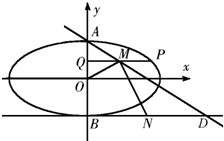 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,A,B分别是C的上下顶点,点B在直线l:y=-1上.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,A,B分别是C的上下顶点,点B在直线l:y=-1上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com