
 ÒŃÖȘÍÖÔČCŁș$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1Łš{aŁŸbŁŸ0}Ł©$”ÄŚóĄąÓÒœč”ă·Ö±đÊÇF1Łš-cŁŹ0Ł©ŁŹF2ŁšcŁŹ0Ł©ŁŹÖ±ÏßlŁșx=my-cÓëÍÖÔČCœ»ÓÚ”ăMŁŹNÁœ”㣏”±m=-$\frac{{\sqrt{3}}}{3}$ŁŹMÊÇÍÖÔČC”Ķ„”㣏ÇÒĄśMF1F2”ÄÖÜł€ÎȘ6Łź
ÒŃÖȘÍÖÔČCŁș$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1Łš{aŁŸbŁŸ0}Ł©$”ÄŚóĄąÓÒœč”ă·Ö±đÊÇF1Łš-cŁŹ0Ł©ŁŹF2ŁšcŁŹ0Ł©ŁŹÖ±ÏßlŁșx=my-cÓëÍÖÔČCœ»ÓÚ”ăMŁŹNÁœ”㣏”±m=-$\frac{{\sqrt{3}}}{3}$ŁŹMÊÇÍÖÔČC”Ķ„”㣏ÇÒĄśMF1F2”ÄÖÜł€ÎȘ6Łź·ÖÎö Łš1Ł©”±m=-$\frac{{\sqrt{3}}}{3}$ʱŁŹżÉ”ĂÖ±Ïßl”ÄÇăбœÇÎȘ$\frac{2ŠĐ}{3}$ŁŹÓÉÌâÒâÁĐčŰÓÚaŁŹc”Ä·œłÌŚéŁŹœâ”ĂaĄąc”ÄÖ”ŁŹœáșÏÒțșŹÌőŒțÇó”ĂbŁŹÔòÍÖÔČC”Ä·œłÌżÉÇóŁ»
Łš2Ł©ÓÉŁš1Ł©Çó”Ăc=1ŁŹÉèÖ±Ïßl”Ä·œłÌÎȘx=my+1ŁŹÁȘÁąÖ±Ïß·œłÌșÍÍÖÔČ·œłÌŁŹ»ŻÎȘčŰÓÚy”ÄÒ»ÔȘ¶țŽÎ·œłÌŁŹÀûÓĂžùÓëÏ”Êę”ÄčŰÏ””Ă”œMĄąN”ÄŚĘŚű±ê”ÄșÍÓë»ęŁŹ
È»șóÏÈÇóÖ±ÏßlÓëxÖáŽčֱʱŁŹMDÓëNE”Äœ»”ăÎȘGŁš$\frac{5}{2}ŁŹ0$Ł©ŁŹÔÙÀûÓĂбÂÊÏà”ÈÖ€”ĂMGč궚”ăGŁš$\frac{5}{2}ŁŹ0$Ł©ŁŹNEÒČč궚”ăGŁš$\frac{5}{2}ŁŹ0$Ł©ŁŹŒŽżÉ˔ÜֱÏßMDÓëNEÏàœ»ÓÚÒ»¶š”㣏žĂ¶š”ă”ÄŚű±êÎȘGŁš$\frac{5}{2}ŁŹ0$Ł©Ł»
Łš3Ł©ÇółöÖ±ÏßAM”Ä·œłÌŁŹ”Ă”œP”ÄŚű±êŁŹÍŹÀíżÉ”ĂQŚű±êŁŹÉèHŁšxŁŹyŁ©ÎȘÒÔPQÎȘÖ±Ÿ¶”ÄÔČÉÏÈÎÒâÒ»”㣏żÉ”Ă$\overrightarrow{PH}•\overrightarrow{QH}=0$ŁŹ”Ă”œÒÔPQÎȘÖ±Ÿ¶”ÄÔȔķœłÌÈĄy=0ŁŹÇó”Ăx=1»òx=7ŁźË”ĂśÒÔPQÎȘÖ±Ÿ¶”ÄÔČșăč꣚1ŁŹ0Ł©Ó룚7ŁŹ0Ł©ŁŹŒŽ”±m±ä»ŻÊ±ŁŹÒÔÏ߶ÎPQÎȘÖ±Ÿ¶”ÄÔȱ»xÖáœŰ”Ă”ÄÏÒł€ÊǶšÖ”6Łź
œâŽđ Łš1Ł©œâŁș”±m=-$\frac{{\sqrt{3}}}{3}$ʱŁŹÖ±Ïßl”ÄÇăбœÇÎȘ$\frac{2ŠĐ}{3}$ŁŹ
ÓÉÌâÒâ”Ă$\left\{\begin{array}{l}{2a+2c=6}\\{\frac{c}{a}=cos\frac{ŠĐ}{3}}\end{array}\right.$ŁŹœâ”Ăa=2ŁŹc=1ŁŹb=$\sqrt{3}$ŁŹ
ĄàÍÖÔČC”Ä·œłÌÎȘ$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$Ł»
Łš2Ł©ÓÉŁš1Ł©ÖȘŁŹc=1ŁŹĄàÖ±Ïßl”Ä·œłÌÎȘx=my+1ŁŹ
ÉèMŁšx1ŁŹy1Ł©ŁŹNŁšx2ŁŹy2Ł©ŁŹ
ÓÉ$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{x=my-1}\end{array}\right.$ŁŹżÉ”ĂŁš3m2+4Ł©y2+6my-9=0Łź
Ąà${y}_{1}+{y}_{2}=\frac{-6m}{3{m}^{2}+4}ŁŹ{y}_{1}{y}_{2}=\frac{-9}{3{m}^{2}+4}$Łź
”±Ö±ÏßlÓëxÖáŽčֱʱŁŹżÉ”ĂMDÓëNE”Äœ»”ăÎȘF2K”ÄÖĐ”ăGŁš$\frac{5}{2}ŁŹ0$Ł©ŁŹ
”±Ö±ÏßlÓëxÖáČ»ŽčֱʱŁŹÏÂĂæրÜMDč궚”ăGŁš$\frac{5}{2}ŁŹ0$Ł©ŁŹ
ÓÉÌâÒâżÉÖȘDŁš4ŁŹy2Ł©ŁŹ
${k}_{GD}=\frac{{y}_{2}}{4-\frac{5}{2}}=\frac{2{y}_{2}}{3}$ŁŹ${k}_{AG}=\frac{{y}_{1}}{{x}_{1}-\frac{5}{2}}=\frac{{y}_{1}}{m{y}_{1}-\frac{3}{2}}$ŁŹ
Ąß${k}_{AG}-{k}_{GD}=\frac{{y}_{1}}{m{y}_{1}-\frac{3}{2}}-\frac{2{y}_{2}}{3}$=$\frac{{y}_{1}}{m{y}_{1}-\frac{3}{2}}-\frac{2}{3}•\frac{-9}{Łš3{m}^{2}+4Ł©{y}_{1}}$
=$\frac{Łš3{m}^{2}+4Ł©{{y}_{1}}^{2}+6Łšm{y}_{1}-\frac{3}{2}Ł©}{Łšm{y}_{1}-\frac{3}{2}Ł©Łš3{m}^{2}+4Ł©{y}_{1}}$=$\frac{Łš3{m}^{2}+4Ł©{{y}_{1}}^{2}+6m{y}_{1}-9}{Łšm{y}_{1}-\frac{3}{2}Ł©Łš3{m}^{2}+4Ł©{y}_{1}}=0$Łź
ĄàkAG=kGDŁŹŒŽMGč궚”ăGŁš$\frac{5}{2}ŁŹ0$Ł©ŁŹ
ÍŹÀíżÉÖ€NEÒČč궚”ăGŁš$\frac{5}{2}ŁŹ0$Ł©ŁŹ
ĄàÖ±ÏßMDÓëNEÏàœ»ÓÚÒ»¶š”㣏žĂ¶š”ă”ÄŚű±êÎȘGŁš$\frac{5}{2}ŁŹ0$Ł©Ł»
Łš3Ł©ÓÉÌâÒâżÉ”ĂÖ±ÏßAM”Ä·œłÌÎȘ$y=\frac{{y}_{1}}{{x}_{1}+2}Łšx+2Ł©$ŁŹ
Áîx=4ŁŹ”ĂP”ăŚű±êÎȘŁš$4ŁŹ\frac{6{y}_{1}}{{x}_{1}+2}$Ł©ŁŹ
ÍŹÀíżÉ”ĂQŁš$4ŁŹ\frac{6{y}_{2}}{{x}_{2}+2}$Ł©ŁŹ
ÉèHŁšxŁŹyŁ©ÎȘÒÔPQÎȘÖ±Ÿ¶”ÄÔČÉÏÈÎÒâÒ»”㣏Ôò$\overrightarrow{PH}•\overrightarrow{QH}=0$ŁŹ
ĄàÒÔPQÎȘÖ±Ÿ¶”ÄÔȔķœłÌÎȘ$Łšx-4Ł©^{2}+Łšy-\frac{6{y}_{1}}{{x}_{1}+2}Ł©Łšy-\frac{6{y}_{2}}{{x}_{2}+2}Ł©=0$Łź
Áîy=0ŁŹÔò$Łšx-4Ł©^{2}+\frac{36{y}_{1}{y}_{2}}{Łšm{y}_{1}+3Ł©Łšm{y}_{2}+3Ł©}=0$Łź
ŒŽ$Łšx-4Ł©^{2}+\frac{36{y}_{1}{y}_{2}}{{m}^{2}{y}_{1}{y}_{2}+3mŁš{y}_{1}+{y}_{2}Ł©+9}=0$ŁŹ
ŒŽ$Łšx-4Ł©^{2}+\frac{36ĄÁ\frac{-9}{3{m}^{2}+4}}{{m}^{2}ĄÁ\frac{-9}{3{m}^{2}+4}+3mĄÁ\frac{-6m}{3{m}^{2}+4}+9}=0$ŁŹ
ŒŽ$Łšx-4Ł©^{2}+\frac{-9ĄÁ36}{-9{m}^{2}-18{m}^{2}+27{m}^{2}+36}=0$Łź
ŒŽŁšx-4Ł©2=9ŁŹœâ”Ăx=1»òx=7Łź
ŒŽÒÔPQÎȘÖ±Ÿ¶”ÄÔČșăč꣚1ŁŹ0Ł©Ó룚7ŁŹ0Ł©ŁŹ
Ąà”±m±ä»ŻÊ±ŁŹÒÔÏ߶ÎPQÎȘÖ±Ÿ¶”ÄÔȱ»xÖáœŰ”Ă”ÄÏÒł€ÊǶšÖ”6Łź
”ăÆÀ ±ŸÌâżŒČéÍÖÔČ·œłÌ”ÄÇ󷚣ŹżŒČéÁËÖ±ÏßÓëÍÖÔČ”ÄλÖĂčŰÏ””ÄÓŠÓĂŁŹŃ”Á·ÁËÀûÓĂбÂÊրÜÈę”ăčČÏßÎÊÌ⣏żŒČéÁËÔȔķœłÌ”ÄÓŠÓĂŁŹÖ±ÏßÓëÇúÏßÁȘÁąŁŹÀûÓĂ·œłÌ”ÄžùÓëÏ”Êę”ÄčŰÏ”ÇóœâŁŹÊÇŽŠÀíŐâÀàÎÊÌâ”ÄŚîÎȘłŁÓÔķœ·šŁŹ”«ÔČŚ¶ÇúÏß”ÄÌŰ”ăÊÇŒÆËăÁż±ÈœÏŽóŁŹÒȘÇóżŒÉúŸß±žœÏÇż”ÄÔËËăÍÆÀí”ÄÄÜÁŠŁŹÊÇŃčÖáÌ⣟


 ÌìÌìÏòÉÏÒ»±ŸșĂŸíÏ”ÁĐŽđ°ž
ÌìÌìÏòÉÏÒ»±ŸșĂŸíÏ”ÁĐŽđ°ž ХѧÉú10·ÖÖÓÓŠÓĂÌâÏ”ÁĐŽđ°ž
ХѧÉú10·ÖÖÓÓŠÓĂÌâÏ”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșÌîżŐÌâ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
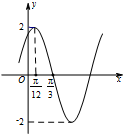 ÒŃÖȘșŻÊęfŁšxŁ©=AsinŁšŠŰx+ŠŐŁ©ŁšAŁŸ0ŁŹŠŰŁŸ0ŁŹ|ŠŐ|ŁŒ$\frac{ŠĐ}{2}$Ł©”ÄČż·ÖÍŒÏóÈçÍŒËùÊŸŁź
ÒŃÖȘșŻÊęfŁšxŁ©=AsinŁšŠŰx+ŠŐŁ©ŁšAŁŸ0ŁŹŠŰŁŸ0ŁŹ|ŠŐ|ŁŒ$\frac{ŠĐ}{2}$Ł©”ÄČż·ÖÍŒÏóÈçÍŒËùÊŸŁźČ鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșŃĄÔńÌâ
| AŁź | 2035 | BŁź | 2036 | CŁź | 4084 | DŁź | 4085 |
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșŃĄÔńÌâ
| AŁź | $\frac{ŠĐ}{6}ĄÜŠÈĄÜ\frac{ŠĐ}{2}$ | BŁź | $\frac{ŠĐ}{3}ĄÜŠÈĄÜ\frac{ŠĐ}{2}$ | CŁź | $0ĄÜŠÈĄÜ\frac{ŠĐ}{3}$ | DŁź | $0ŁŒŠÈŁŒ\frac{2ŠĐ}{3}$ |
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
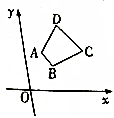 ÒŃÖȘÌĘĐÎABCDŁŹÈçÍŒËùÊŸŁŹÆäÖĐABĄÎCDŁŹÇÒDC=2ABŁŹÈęžö¶„”ă”ÄŚű±ê·Ö±đÎȘAŁš1ŁŹ2Ł©ĄąBŁš2ŁŹ1Ł©ĄąCŁš4ŁŹ2Ł©ŁŹÇó”ăD”ÄŚű±êŁź
ÒŃÖȘÌĘĐÎABCDŁŹÈçÍŒËùÊŸŁŹÆäÖĐABĄÎCDŁŹÇÒDC=2ABŁŹÈęžö¶„”ă”ÄŚű±ê·Ö±đÎȘAŁš1ŁŹ2Ł©ĄąBŁš2ŁŹ1Ł©ĄąCŁš4ŁŹ2Ł©ŁŹÇó”ăD”ÄŚű±êŁźČ鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com