
分析 (1)求导数,可得2a=$\frac{1}{x}$+2x在(0,+∞)上有解,求出a的范围,再验证即可得出结论;
(2)2x2-2ax+1=0的两个根为x=$\frac{1}{2}$(a±$\sqrt{{a}^{2}-2}$),求出极值.即可证明结论.
解答 (1)解:∵f(x)=lnx+(x-a)2,
∴f′(x)=$\frac{1}{x}$+2(x-a)=0,即2a=$\frac{1}{x}$+2x在(0,+∞)上有解,
∴2a≥2$\sqrt{2}$,
∴a≥$\sqrt{2}$,
a=$\sqrt{2}$时,f′(x)>0,函数无极值,
∴a>$\sqrt{2}$;
(2)证明:f′(x)=$\frac{1}{x}$+2(x-a)=0,即2x2-2ax+1=0的两个根为x=$\frac{1}{2}$(a±$\sqrt{{a}^{2}-2}$),
∴f(x)的所有极值和=ln$\frac{1}{2}$(a+$\sqrt{{a}^{2}-2}$)+[$\frac{1}{2}$(-a+$\sqrt{{a}^{2}-2}$)]2-2+ln$\frac{1}{2}$(a-$\sqrt{{a}^{2}-2}$)+[$\frac{1}{2}$(-a-$\sqrt{{a}^{2}-2}$)]2=ln$\frac{1}{2}$+a2-1>1-ln2=ln$\frac{e}{2}$.
点评 本题考查导数知识的综合运用,考查函数的极值,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD为梯形,AB∥CD,PD⊥平面ABCD,∠BAD=∠ADC=90°,DC=2AB=2a,DA=$\sqrt{3}a$,E为BC中点.
如图,四边形ABCD为梯形,AB∥CD,PD⊥平面ABCD,∠BAD=∠ADC=90°,DC=2AB=2a,DA=$\sqrt{3}a$,E为BC中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
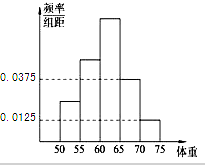 某校为了提高学生的身体素质,决定组建学校足球队,学校为了解学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12.
某校为了提高学生的身体素质,决定组建学校足球队,学校为了解学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别是F1(-c,0),F2(c,0),直线l:x=my-c与椭圆C交于点M,N两点,当m=-$\frac{{\sqrt{3}}}{3}$,M是椭圆C的顶点,且△MF1F2的周长为6.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别是F1(-c,0),F2(c,0),直线l:x=my-c与椭圆C交于点M,N两点,当m=-$\frac{{\sqrt{3}}}{3}$,M是椭圆C的顶点,且△MF1F2的周长为6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com