
 如图,四边形ABCD为梯形,AB∥CD,PD⊥平面ABCD,∠BAD=∠ADC=90°,DC=2AB=2a,DA=$\sqrt{3}a$,E为BC中点.
如图,四边形ABCD为梯形,AB∥CD,PD⊥平面ABCD,∠BAD=∠ADC=90°,DC=2AB=2a,DA=$\sqrt{3}a$,E为BC中点.分析 (1)连接BD,便可得到BD=DC,而E又是BC中点,从而得到BC⊥DE,而由PD⊥平面ABCD便可得到BC⊥PD,从而得出BC⊥平面PDE,根据面面垂直的判定定理即可得出平面PBC⊥平面PDE;
(2)连接AC,交BD于O,根据相似三角形的比例关系即可得到AO=$\frac{1}{2}OC$,从而在PC上找F,使得PF=$\frac{1}{2}FC$,连接OF,从而可说明PA∥平面BDF,这样即找到了满足条件的F点.
解答 解:(1)证明:连结BD,∠BAD=90°,$AB=a,DA=\sqrt{3}a$;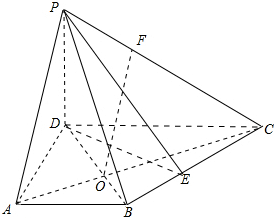
∴BD=DC=2a,E为BC中点,∴BC⊥DE;
又PD⊥平面ABCD,BC?平面ABCD;
∴BC⊥PD,DE∩PD=D;
∴BC⊥平面PDE;
∵BC?平面PBC;
∴平面PBC⊥平面PDE;
(2)如上图,连结AC,交BD于O点,则:△AOB∽△COD;
∵DC=2AB;
∴$\frac{AB}{DC}=\frac{AO}{OC}=\frac{1}{2}$;
∴$AO=\frac{1}{2}OC$;
∴在PC上取F,使$PF=\frac{1}{2}FC$;
连接OF,则OF∥PA,而OF?平面BDF,PA?平面BDF;
∴PA∥平面BDF.
点评 考查直角三角形边的关系,等腰三角形中线也是高线,以及线面垂直的性质,线面垂直的判定定理,相似三角形边的比例关系,线面平行的判定定理.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
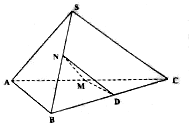 已知三棱锥S-ABC中△SAB与△ABC均为等边三角形,M、N分别为AC、SB的中点,经过M、N且与AB平行的平面α与BC交于点D.
已知三棱锥S-ABC中△SAB与△ABC均为等边三角形,M、N分别为AC、SB的中点,经过M、N且与AB平行的平面α与BC交于点D.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知点p(c,$\frac{3}{2}$c)在以F(c,0)为右焦点的椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,斜率为1的直线m过点F与椭圆Γ交于A,B两点,且与直线l:x=4c交于点M.
已知点p(c,$\frac{3}{2}$c)在以F(c,0)为右焦点的椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,斜率为1的直线m过点F与椭圆Γ交于A,B两点,且与直线l:x=4c交于点M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
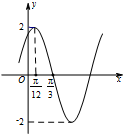 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
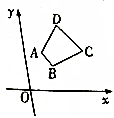 已知梯形ABCD,如图所示,其中AB∥CD,且DC=2AB,三个顶点的坐标分别为A(1,2)、B(2,1)、C(4,2),求点D的坐标.
已知梯形ABCD,如图所示,其中AB∥CD,且DC=2AB,三个顶点的坐标分别为A(1,2)、B(2,1)、C(4,2),求点D的坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com