
分析 (1)通过将点($\frac{3}{2}$,1)代入椭圆方程、并利用a2-b2=1,计算即得结论;
(2)分MN斜率不存在与存在两种情况讨论,当点P不在y轴上时,分别联立直线PA1方程、直线PA2方程与椭圆方程,计算出kQM、kQN即可.
解答 解:(1)∵椭圆C:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}=1$(a>b>0)经过点($\frac{3}{2}$,1),
∴$\frac{1}{{a}^{2}}+\frac{(\frac{3}{2})^{2}}{{b}^{2}}=1$ ①
又∵椭圆的一个焦点是F(0,1),
∴a2-b2=1 ②
由①②得:a2=4,b2=3,
∴椭圆C的方程为:$\frac{{y}^{2}}{4}+\frac{{x}^{2}}{3}=1$;
(2)结论:直线MN恒经过定点Q(0,1).
证明如下:
由(1)知a2=4,∴点P在直线y=4上,设P(t,4).
当MN斜率不存在时,直线MN即y轴,通过点Q(0,1);
当点P不在y轴上时,记A1(0,2)、A2(0,-2),M(x1,y1),N(x2,y2),
则直线PA1方程:y=$\frac{4-2}{t-0}$x+2=$\frac{2}{t}$x+2,直线PA2方程:y=$\frac{4-(-2)}{t-0}$x-2=$\frac{6}{t}$x-2,
联立$\left\{\begin{array}{l}{y=\frac{2}{t}x+2}\\{\frac{{y}^{2}}{4}+\frac{{x}^{2}}{3}=1}\end{array}\right.$,得:(3+t2)x2+6tx=0,
解得x1=-$\frac{6t}{3+{t}^{2}}$,y1=$\frac{2{t}^{2}-6}{3+{t}^{2}}$,∴kQM=$\frac{{y}_{1}-1}{{x}_{1}}$=$\frac{9-{t}^{2}}{6t}$,
联立$\left\{\begin{array}{l}{y=\frac{6}{t}x-2}\\{\frac{{y}^{2}}{4}+\frac{{x}^{2}}{3}=1}\end{array}\right.$,得:(27+t2)x2-18tx=0
解得x2=$\frac{18t}{27+{t}^{2}}$,y2=$\frac{54-2{t}^{2}}{27+{t}^{2}}$,∴kQN=$\frac{{y}_{2}-1}{{x}_{2}}$=$\frac{9-{t}^{2}}{6t}$,
∵kQM=$\frac{9-{t}^{2}}{6t}$=kQN,
∴直线MN恒经过定点Q(0,1).
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,考查分类讨论的思想,注意解题方法的积累,属于中档题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:填空题
 如图所示,平行四边形ABCD中,AE,CF分别是∠BAD,∠BCD的平分线,根据现有的图形请添加一个条件,使四边形AECF是菱形,则添加的一个条件可以是AC⊥EF(只写出一个即可)
如图所示,平行四边形ABCD中,AE,CF分别是∠BAD,∠BCD的平分线,根据现有的图形请添加一个条件,使四边形AECF是菱形,则添加的一个条件可以是AC⊥EF(只写出一个即可)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图在以OA为半径的半圆M中,有三个半径为1的相同的半圆,在半圆M中任取一点N.
如图在以OA为半径的半圆M中,有三个半径为1的相同的半圆,在半圆M中任取一点N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
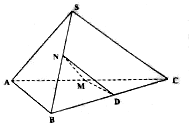 已知三棱锥S-ABC中△SAB与△ABC均为等边三角形,M、N分别为AC、SB的中点,经过M、N且与AB平行的平面α与BC交于点D.
已知三棱锥S-ABC中△SAB与△ABC均为等边三角形,M、N分别为AC、SB的中点,经过M、N且与AB平行的平面α与BC交于点D.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (π,$\frac{9π}{8}$) | B. | [π,$\frac{9π}{8}$] | C. | [$\frac{7π}{6}$,$\frac{4π}{3}$] | D. | ($\frac{7π}{6}$,$\frac{4π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
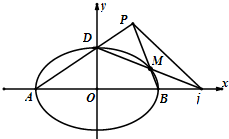 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,-2),且离心率为$\frac{{\sqrt{5}}}{3}$.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,-2),且离心率为$\frac{{\sqrt{5}}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com