
分析 取AB的中点为D,求得CD、PD的值,由题意可得$\frac{a}{b}$<1①,根据PD>0求得$\frac{a}{b}$>$\frac{1}{2}$ ②.再根据△PCD中,任意两边之和大于第三边,求得$\sqrt{2-\sqrt{3}}$<$\frac{a}{b}$<$\sqrt{2+\sqrt{3}}$ ③.综合①②③可得$\frac{a}{b}$的范围.
解答 解:取AB的中点为D,则由PA=PB=a,PC=AB=BC=CA=b,且a<b,
可得CD⊥AB,PD⊥AB,∴CD=$\sqrt{{BC}^{2}{-BD}^{2}}$=$\frac{\sqrt{3}}{2}$b,PD=$\sqrt{{PA}^{2}{-AD}^{2}}$=$\sqrt{{a}^{2}-\frac{{b}^{2}}{4}}$,$\frac{a}{b}$<1①,
∴a2-$\frac{{b}^{2}}{4}$>0,求得$\frac{a}{b}$>$\frac{1}{2}$ ②.
根据△PCD中,任意两边之和大于第三边,可得$\left\{\begin{array}{l}{\sqrt{{a}^{2}-\frac{{b}^{2}}{4}}+\frac{\sqrt{3}}{2}b>b}\\{b+\frac{\sqrt{3}}{2}b>\sqrt{{a}^{2}-\frac{{b}^{2}}{4}}}\\{\sqrt{{a}^{2}-\frac{{b}^{2}}{4}}+b>\frac{\sqrt{3}}{2}b}\end{array}\right.$,
求得(2-$\sqrt{3}$)b2<a2<(2+$\sqrt{3}$)b2,故有$\sqrt{2-\sqrt{3}}$<$\frac{a}{b}$<$\sqrt{2+\sqrt{3}}$=$\frac{\sqrt{6}-\sqrt{2}}{2}$ ③.
综合①②③可得$\frac{\sqrt{6}-\sqrt{2}}{2}$<$\frac{a}{b}$<1,
故答案为:($\frac{\sqrt{6}-\sqrt{2}}{2}$,1).
点评 本题主要考查棱锥的结构特征,三角形任意两边之和大于第三边,解根式不等式,体现了转化的数学思想,属于中档题.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n2 | B. | n2+n | C. | 2n-1 | D. | 2n+1-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
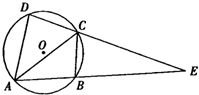 如图所示,四边形ABCD的外接圆为圆O,线段AB与线段DC的延长线交于点E,$\frac{AD}{DE}$=$\frac{1}{3}$.
如图所示,四边形ABCD的外接圆为圆O,线段AB与线段DC的延长线交于点E,$\frac{AD}{DE}$=$\frac{1}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com