
| A. | (π,$\frac{9π}{8}$) | B. | [π,$\frac{9π}{8}$] | C. | [$\frac{7π}{6}$,$\frac{4π}{3}$] | D. | ($\frac{7π}{6}$,$\frac{4π}{3}$) |
分析 利用三角函数的倍角公式、积化和差与和差化积公式化简已知的等式,根据公差d的范围求出公差的值,代入前n项和公式后利用二次函数的对称轴的范围求解首项a1取值范围.
解答 解:∵$\frac{si{n}^{2}{a}_{4}-co{s}^{2}{a}_{4}+co{s}^{2}{a}_{4}co{s}^{2}{a}_{8}-si{n}^{2}{a}_{4}si{n}^{2}{a}_{8}}{sin({a}_{5}+{a}_{7})}$
=$\frac{-cos2{a}_{4}+(cos{a}_{4}cos{a}_{8}-sin{a}_{4}sin{a}_{8})(cos{a}_{4}cos{a}_{8}+sin{a}_{4}sin{a}_{8})}{sin({a}_{5}+{a}_{7})}$
=$\frac{-cos2{a}_{4}+cos({a}_{4}+{a}_{8})cos({a}_{4}-{a}_{8})}{sin({a}_{5}+{a}_{7})}$
=$\frac{\frac{1}{2}cos2{a}_{4}+\frac{1}{2}cos2{a}_{8}-cos2{a}_{4}}{sin({a}_{5}+{a}_{7})}$
=$\frac{\frac{1}{2}(cos2{a}_{8}-cos2{a}_{4})}{sin({a}_{5}+{a}_{7})}$
=$\frac{\frac{1}{2}×(-2)sin({a}_{8}+{a}_{4})sin({a}_{8}-{a}_{4})}{sin({a}_{5}+{a}_{7})}$
=-$\frac{sin({a}_{8}+{a}_{4})sin({a}_{8}-{a}_{4})}{sin({a}_{4}+{a}_{8})}$
=-sin(4d),
∴sin(4d)=-1,
∵d∈(-1,0),∴4d∈(-4,0),
∴4d=-$\frac{π}{2}$,d=-$\frac{π}{8}$,
∵Sn=na1+$\frac{n(n-1)}{2}•d$=$n{•a}_{1}+\frac{n(n-1)}{2}•(-\frac{π}{8})$=-$\frac{π}{16}{n}^{2}$+$({a}_{1}+\frac{π}{16})n$,
∴其对称轴方程为:n=$\frac{8}{π}$$({a}_{1}+\frac{π}{16})$,
有题意可知当且仅当n=9时,数列{an}的前n项和Sn取得最大值,
∴$\frac{17}{2}$<$\frac{8}{π}$$({a}_{1}+\frac{π}{16})$<$\frac{19}{2}$,解得π<a1<$\frac{9}{8}π$,
故选:A.
点评 本题考查等差数列的通项公式,考查三角函数的有关公式,考查等差数列的前n项和,训练二次函数取得最值得条件,考查运算求解能力,注意解题方法的积累,属于中档题.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
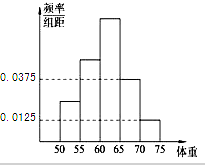 某校为了提高学生的身体素质,决定组建学校足球队,学校为了解学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12.
某校为了提高学生的身体素质,决定组建学校足球队,学校为了解学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com