
分析 设F(c,0),P(m,n),(m<0),设PF的中点为M(0,b),即有m=-c,n=2b,将中点M的坐标代入双曲线方程,求出a与b的关系,即可求出双曲线C的渐近线方程.
解答 解:设F(c,0),P(m,n),(m<0),
设PF的中点为M(0,b),
即有m=-c,n=2b,
将点(-c,2b)代入双曲线方程可得,
$\frac{{c}^{2}}{{a}^{2}}$-$\frac{4{b}^{2}}{{b}^{2}}$=1,
又c2=a2+b2,
∴$\frac{{b}^{2}}{{a}^{2}}$=4,
∴$\frac{b}{a}$=2,
∴双曲线C的渐近线方程为y=±2x,
故答案为:y=±2x
点评 本题考查双曲线的方程和性质,主要考查双曲线的渐近线方程的求法,同时考查中点坐标公式的运用,属于中档题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
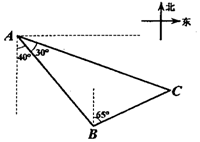 如图所示,一艘海轮从A处出发,以每小时40海里的速度沿南偏东40°方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是南偏东70°,在B处观察灯塔,其方向是北偏东65°,那么B、C两点间的距离是10$\sqrt{2}$海里.
如图所示,一艘海轮从A处出发,以每小时40海里的速度沿南偏东40°方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是南偏东70°,在B处观察灯塔,其方向是北偏东65°,那么B、C两点间的距离是10$\sqrt{2}$海里.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 16 | C. | 12 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com