
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
科目:高中数学 来源: 题型:解答题
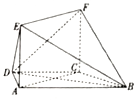 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
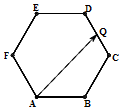
| A. | $\overrightarrow{AB}•\overrightarrow{AQ}$ | B. | $\overrightarrow{AC}•\overrightarrow{AQ}$ | C. | $\overrightarrow{AD}•\overrightarrow{AQ}$ | D. | $\overrightarrow{AE}•\overrightarrow{AQ}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
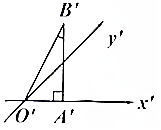
| A. | $\sqrt{6}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b<a<c | B. | c<b<a | C. | c<a<b | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
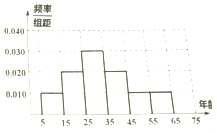 2016年3月31日贵州省第十二届人民代表大会常务委员会第二十一次会议通过的《贵州省人口与计划生育条例》全面开放二孩政策.为了了解人们对于贵州省新颁布的“生育二孩放开”政策的热度,现在某市进行调查,对[5,65]岁的人群随机抽取了n人,得到如下统计表和各年龄段抽取人数频率分布直方图:
2016年3月31日贵州省第十二届人民代表大会常务委员会第二十一次会议通过的《贵州省人口与计划生育条例》全面开放二孩政策.为了了解人们对于贵州省新颁布的“生育二孩放开”政策的热度,现在某市进行调查,对[5,65]岁的人群随机抽取了n人,得到如下统计表和各年龄段抽取人数频率分布直方图:| 分组 | 支持“生育二孩”人数 | 占本组的频率 |
| [5,15) | 4 | 0.8 |
| [15,25) | 5 | p |
| [2,35) | 12 | 0.8 |
| [35,45) | 8 | 0.8 |
| [45,55) | 2 | 0.4 |
| [55,65) | 1 | 0.2 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 支持 | 3 | 29 | 32 |
| 不支持 | 7 | 11 | 18 |
| 合计 | 10 | 40 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com