
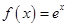 .
.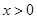 时,设
时,设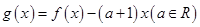 .讨论函数
.讨论函数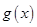 的单调性;
的单调性;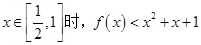 .
.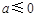 时,
时,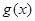 在
在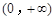 上是增函数;
上是增函数;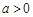 时,
时,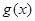 在
在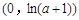 上是减函数,在
上是减函数,在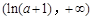 上是增函数.
上是增函数.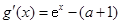 ,当
,当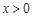 时,
时,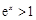 .
.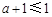 ,即
,即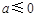 时,当
时,当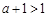 ,即
,即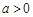 时,即得结论;
时,即得结论;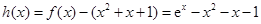 ,由于导数,通过确定函数的单调性及最值,达到解题目的.
,由于导数,通过确定函数的单调性及最值,达到解题目的.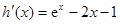 ,
,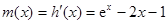 ,再次利用导数加以研究
,再次利用导数加以研究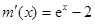 ,
, 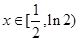 时,
时, 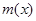 在
在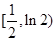 上是减函数,
上是减函数,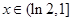 时,
时, 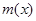 在
在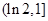 上是增函数,
上是增函数,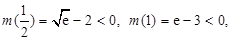
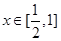 时,恒有
时,恒有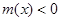 ,即
,即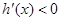 ,
,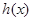 在
在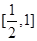 上为减函数,由
上为减函数,由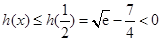 ,得证.
,得证.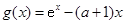 ,所以
,所以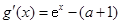 . 2分
. 2分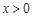 时,
时,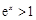 ,故有:
,故有: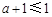 ,即
,即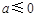 时,
时,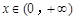 ,
,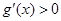 ;
;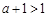 ,即
,即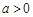 时,
时,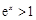 ,
,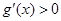 ,得
,得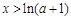 ;令
;令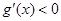 ,得
,得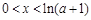 , 5分
, 5分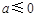 时,
时,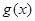 在
在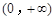 上是增函数;
上是增函数;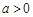 时,
时,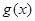 在
在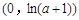 上是减函数,在
上是减函数,在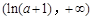 上是增函数. 6分
上是增函数. 6分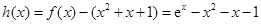 ,则
,则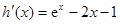 ,
,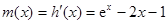 ,则
,则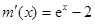 , 8分
, 8分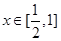 ,所以当
,所以当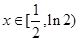 时,
时,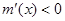 ;
;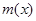 在
在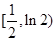 上是减函数,
上是减函数,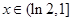 时,
时,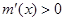 ,
,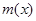 在
在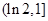 上是增函数,
上是增函数,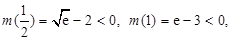 所以当
所以当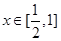 时,恒有
时,恒有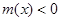 ,即
,即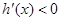 ,
,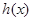 在
在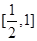 上为减函数,所以
上为减函数,所以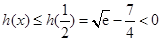 ,
,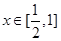 时,
时,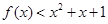 . 13分
. 13分

 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源:不详 题型:解答题
 的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)
的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计) (弧度),将绿化带总长度表示为
(弧度),将绿化带总长度表示为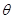 的函数
的函数 ;
;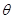 的值,使得绿化带总长度最大.
的值,使得绿化带总长度最大.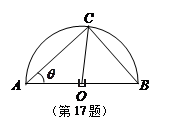
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
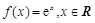 .
. 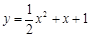 有唯一公共点.
有唯一公共点. 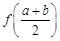 与
与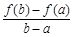 的大小, 并说明理由.
的大小, 并说明理由. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com