练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某学生在一门功课的22次考试中，所得分数茎叶图如图所示，则此学生该门功课考试分数的极差与中位数之和为（ ）

    A.117
    B.118
    C.118.5
    D.119.5

    【答案】B
    【解析】解：22次考试分数最大为98，最小为56，所以极差为98﹣56=42，
    从小到大排列，中间两数为76，76，所以中位数为76．
    所以此学生该门功课考试分数的极差与中位数之和为42+76=118．
    故选B．
    【考点精析】关于本题考查的茎叶图，需要了解茎叶图又称“枝叶图”，它的思路是将数组中的数按位数进行比较，将数的大小基本不变或变化不大的位作为一个主干（茎），将变化大的位的数作为分枝（叶），列在主干的后面，这样就可以清楚地看到每个主干后面的几个数，每个数具体是多少才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某研究所计划利用宇宙飞船进行新产品搭载试验，计划搭载若干件新产品A，B，该研究所要根据产品的研制成本、产品重量、搭载试验费用和预计收益来决定具体安排，通过调查得到的有关数据如表：

    每件A产品

    每件B产品

    研制成本、搭载试验费用之和（万元）

    20

    30

    产品重量（千克）

    10

    5

    预计收益（万元）

    80

    60

    已知研制成本、搭载试验费用之和的最大资金为300万元，最大搭载重量为110千克，则如何安排这两种产品进行搭载，才能使总预计收益达到最大，求最大预计收益是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，已知2sinBcosA=sin（A+C）．
    （1）求角A；
    （2）若BC=2，△ABC的面积是 ，求AB．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足an+1=2an﹣1（n∈N+），a1=2．
    （1）求证：数列{an﹣1}为等比数列，并求数列{an}的通项公式；
    （2）求数列{nan}的前n项和Sn（n∈N+）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（1）在等差数列中，已知，前项和为，且，求当取何值时， 取得最大值，并求出它的最大值；

    （2）已知数列的通项公式是，求数列的前项和.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量 与向量 =（2，﹣1，2）共线，且满足 =18，（k + ）⊥（k ﹣ ），求向量 及k的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，QA=AB= PD．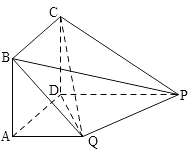

    （1）证明：平面PQC⊥平面DCQ
    （2）求二面角Q﹣BP﹣C的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=cos2（x+ ），g（x）=1+ sin2x．
    （1）设x=x0是函数y=f（x）图象的一条对称轴，求g（x0）的值．
    （2）设函数h（x）=f（x）+g（x），若不等式|h（x）﹣m|≤1在[﹣ ， ]上恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】根据下列条件，求直线的方程：
    （Ⅰ）过直线l1：2x﹣3y﹣1=0和l2：x+y+2=0的交点，且垂直于直线2x﹣y+7=0；
    （Ⅱ）过点（﹣3，1），且在两坐标轴上的截距之和为﹣4．

    查看答案和解析>>

    同步练习册答案