练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知向量 与向量 =（2，﹣1，2）共线，且满足 =18，（k + ）⊥（k ﹣ ），求向量 及k的值．

    【答案】解：∵ ， 共线，∴存在实数λ，使 =λ ，
    ∴ =λ 2=λ| |2 ， 解得λ=2．
    ∴ =2 =（4，﹣2，4）．
    ∵（k + ）⊥（k ﹣ ），
    ∴（k + ）（k ﹣ ）=（k +2 ）（k ﹣2 ）=0，
    即（k2﹣4）| |2=0，
    解得k=±2
    【解析】由已知得存在实数λ，使 =λ ，由此能求出 =2 =（4，﹣2，4）．由（k + ）⊥（k ﹣ ），得（k2﹣4）| |2=0，由此能求出k=±2．
    【考点精析】关于本题考查的数量积判断两个平面向量的垂直关系，需要了解若平面的法向量为，平面的法向量为，要证，只需证，即证;即：两平面垂直两平面的法向量垂直才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知数列是公差为正数的等差数列，其前项和为，且， ．

    （1）求数列的通项公式；

    （2）数列满足， .①求数列的通项公式；②是否存在正整数， （），使得， ， 成等差数列？若存在，求出， 的值；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

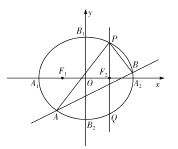
    【题目】如图，已知椭圆的左、右顶点分别为，上、下顶点分别为，两个焦点分别为， ，四边形的面积是四边形的面积的2倍.

    （1）求椭圆的方程；

    （2）过椭圆的右焦点且垂直于轴的直线交椭圆于两点， 是椭圆上位于直线两侧的两点.若直线过点，且，求直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设椭圆的中心在原点，焦点在x轴上，离心率 ．已知点 到这个椭圆上的点的最远距离为 ，求这个椭圆方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学生在一门功课的22次考试中，所得分数茎叶图如图所示，则此学生该门功课考试分数的极差与中位数之和为（ ）

    A.117
    B.118
    C.118.5
    D.119.5

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数.

    （1）当时，求的单调区间；

    （2）若的图象与轴交于两点，起，求的取值范围；

    （3）令， ，证明： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若f（x+1）的定义域为[0，1]，则函数f（2x﹣2）的定义域为（ ）
    A.[log23，2]
    B.[0，1]
    C.
    D.[0，2]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，梯形ABCD中，AD∥BC，AD⊥AB，AD=1，BC=2，AB=3，P是AB上的一个动点，∠CPB=α，∠DPA=β． （Ⅰ）当 最小时，求tan∠DPC的值；
    （Ⅱ）当∠DPC=β时，求 的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    (1)若，试判断函数的零点个数；

    (2)若函数在上为增函数，求整数的最大值，(可能要用的数据: ； ).

    查看答案和解析>>

    同步练习册答案