
【题目】设椭圆的中心在原点,焦点在x轴上,离心率 ![]() .已知点
.已知点 ![]() 到这个椭圆上的点的最远距离为
到这个椭圆上的点的最远距离为 ![]() ,求这个椭圆方程.
,求这个椭圆方程.
【答案】解:设椭圆方程为 ![]() ,M(x,y)为椭圆上的点,由
,M(x,y)为椭圆上的点,由 ![]() 得a=2b,
得a=2b, ![]() ,
,
若﹣b>﹣ ![]() 即
即 ![]() ,则当y=﹣b时|PM|2最大,即
,则当y=﹣b时|PM|2最大,即 ![]() ,
,
∴b= ![]() ,故矛盾.
,故矛盾.
若﹣b≤﹣ ![]() ≤b,即
≤b,即 ![]() 时,
时, ![]() 时,
时,
4b2+3=7,
b2=1,从而a2=4.
所求方程为 ![]()
【解析】先设椭圆方程为 ![]() ,M(x,y)为椭圆上的点,由离心率得a=2b,利用两点间的距离公式表示出|PM|2若
,M(x,y)为椭圆上的点,由离心率得a=2b,利用两点间的距离公式表示出|PM|2若 ![]() ,则当y=﹣b时|PM|2最大,这种情况不可能;若
,则当y=﹣b时|PM|2最大,这种情况不可能;若 ![]() 时,
时, ![]() 时4b2+3=7,从而求出b值,最后求得所求方程.
时4b2+3=7,从而求出b值,最后求得所求方程.
【考点精析】关于本题考查的椭圆的概念和椭圆的标准方程,需要了解平面内与两个定点![]() ,
,![]() 的距离之和等于常数(大于
的距离之和等于常数(大于![]() )的点的轨迹称为椭圆,这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距;椭圆标准方程焦点在x轴:
)的点的轨迹称为椭圆,这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距;椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能得出正确答案.
才能得出正确答案.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
【题目】已知圆x2+y2=4上一定点A(2,0),B(1,1)为圆内一点,P,Q为圆上的动点. 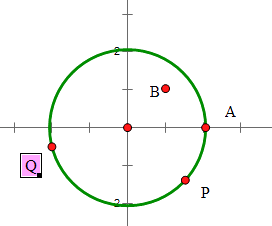
(1)求线段AP中点的轨迹方程;
(2)若∠PBQ=90°,求线段PQ中点的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an+1=2an﹣1(n∈N+),a1=2.
(1)求证:数列{an﹣1}为等比数列,并求数列{an}的通项公式;
(2)求数列{nan}的前n项和Sn(n∈N+).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】供电部门对某社区![]() 位居民2016年11月份人均用电情况进行统计后,按人均用电量分为
位居民2016年11月份人均用电情况进行统计后,按人均用电量分为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 五组,整理得到如下的频率分布直方图,则下列说法错误的是( )
五组,整理得到如下的频率分布直方图,则下列说法错误的是( )
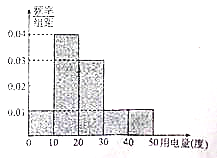
A. 11月份人均用电量人数最多的一组有![]() 人
人
B. 11月份人均用电量不低于![]() 度的有
度的有![]() 人
人
C. 11月份人均用电量为![]() 度
度
D. 在这![]() 位居民中任选
位居民中任选![]() 位协助收费,选到的居民用电量在
位协助收费,选到的居民用电量在![]() 一组的概率为
一组的概率为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com