
【题目】已知圆x2+y2=4上一定点A(2,0),B(1,1)为圆内一点,P,Q为圆上的动点. 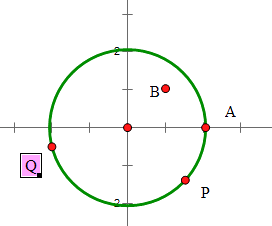
(1)求线段AP中点的轨迹方程;
(2)若∠PBQ=90°,求线段PQ中点的轨迹方程.
【答案】
(1)解:设AP中点为M(x,y),
由中点坐标公式可知,P点坐标为(2x﹣2,2y)
∵P点在圆x2+y2=4上,∴(2x﹣2)2+(2y)2=4.
故线段AP中点的轨迹方程为(x﹣1)2+y2=1
(2)解:设PQ的中点为N(x,y),
在Rt△PBQ中,|PN|=|BN|,
设O为坐标原点,则ON⊥PQ,
所以|OP|2=|ON|2+|PN|2=|ON|2+|BN|2,
所以x2+y2+(x﹣1)2+(y﹣1)2=4.
故线段PQ中点的轨迹方程为x2+y2﹣x﹣y﹣1=0.
【解析】(1)设出AP的中点坐标,利用中点坐标公式求出P的坐标,据P在圆上,将P坐标代入圆方程,求出中点的轨迹方程.(2)利用直角三角形的中线等于斜边长的一半得到|PN|=|BN|,利用圆心与弦中点连线垂直弦,利用勾股定理得到
|OP|2=|ON|2+|PN|2 , 利用两点距离公式求出动点的轨迹方程.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:
【题目】若直线l1:y=x,l2:y=x+2与圆C:x2+y2﹣2mx﹣2ny=0的四个交点把圆C分成的四条弧长相等,则m=( )
A.0或1
B.0或﹣1
C.1或﹣1
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,2)为圆C:x2+y2﹣2ax﹣2ay=0(a>0)外一点,圆C上存在点P使得∠CAP=45°,则实数a的取值范围是( )
A.(0,1)
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,
, ![]() .
.
(1)当n=1,2,3时,分别比较f(n)与g(n)的大小(直接给出结论);
(2)由(1)猜想f(n)与g(n)的大小关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ln(3﹣x)(x+1)的定义域为( )
A.[﹣1,3]
B.(﹣1,3)
C.(﹣∞,﹣3)∪(1,+∞)
D.(﹣∞,﹣1)∪(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是公差为正数的等差数列,其前
是公差为正数的等差数列,其前![]() 项和为
项和为![]() ,且
,且![]() ,
, ![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)数列![]() 满足
满足![]() ,
, ![]() .①求数列
.①求数列![]() 的通项公式;②是否存在正整数
的通项公式;②是否存在正整数![]() ,
, ![]() (
(![]() ),使得
),使得![]() ,
, ![]() ,
, ![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() ,
, ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=2sin4x+2cos4x+cos22x﹣3.
(1)求函数f(x)的最小正周期.
(2)求函数f(x)在闭区间[ ![]() ]上的最小值并求当f(x)取最小值时,x的取值集合.
]上的最小值并求当f(x)取最小值时,x的取值集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com