
【题目】如图,梯形ABCD中,AD∥BC,AD⊥AB,AD=1,BC=2,AB=3,P是AB上的一个动点,∠CPB=α,∠DPA=β. (Ⅰ)当 ![]() 最小时,求tan∠DPC的值;
最小时,求tan∠DPC的值;
(Ⅱ)当∠DPC=β时,求 ![]() 的值.
的值.
【答案】解:(Ⅰ)以A为原点,AB所在直线为x轴, 建立如图所示的直角坐标系.
则A(0,0),B(3,0),C(3,2),
D(0,1),令P(x,0),0≤x≤3
有 ![]()
所以 ![]() ,
,
当 ![]() 时,
时, ![]() 最小
最小
此时 ![]() ,在△CPB中,
,在△CPB中, 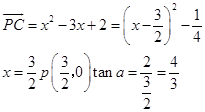 ,
,
在△DPA中, 
所以 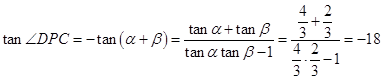 ,
,
(Ⅱ)由(Ⅰ)知, ![]() ,
,![]() ,
,
∵∠DPC=β,∴α=π﹣2β,tanα=﹣tan2β
∴ 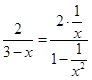 整理得:
整理得: ![]()
此时 ![]() .
.
【解析】(I)以A为原点,AB所在直线为x轴,分别写出点A,B,C,D,P的坐标,利用数量积和二次函数的单调性\两角和的正切公式即可得出;(II)利用诱导公式和倍角公式即可得出.
【考点精析】本题主要考查了两角和与差的正切公式的相关知识点,需要掌握两角和与差的正切公式:![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos2(x+ ![]() ),g(x)=1+
),g(x)=1+ ![]() sin2x.
sin2x.
(1)设x=x0是函数y=f(x)图象的一条对称轴,求g(x0)的值.
(2)设函数h(x)=f(x)+g(x),若不等式|h(x)﹣m|≤1在[﹣ ![]() ,
, ![]() ]上恒成立,求实数m的取值范围.
]上恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程C:x2+y2﹣2x﹣4y+m=0,
(1)若方程C表示圆,求实数m的范围;
(2)在方程表示圆时,该圆与直线l:x+2y﹣4=0相交于M、N两点, ![]() ,求m的值;
,求m的值;
(3)在(2)的条件下,定点A(1,0),P在线段MN上运动,求直线AP的斜率取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】供电部门对某社区![]() 位居民2016年11月份人均用电情况进行统计后,按人均用电量分为
位居民2016年11月份人均用电情况进行统计后,按人均用电量分为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 五组,整理得到如下的频率分布直方图,则下列说法错误的是( )
五组,整理得到如下的频率分布直方图,则下列说法错误的是( )
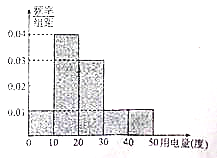
A. 11月份人均用电量人数最多的一组有![]() 人
人
B. 11月份人均用电量不低于![]() 度的有
度的有![]() 人
人
C. 11月份人均用电量为![]() 度
度
D. 在这![]() 位居民中任选
位居民中任选![]() 位协助收费,选到的居民用电量在
位协助收费,选到的居民用电量在![]() 一组的概率为
一组的概率为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com