
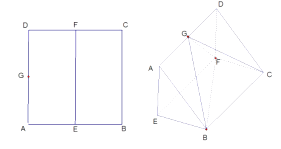
【题目】如图所示,正方体 ![]() 中,
中, ![]() 分别是
分别是 ![]() 的中点,将
的中点,将 ![]() 沿
沿 ![]() 折起,使
折起,使 ![]() .
.
(1)证明: ![]() 平面
平面 ![]() ;
;
(2)求二面角 ![]() 的余弦值.
的余弦值.
【答案】
(1)证明:设正方体的棱长为2,
在 ![]() 中,
中, ![]() ,
, ![]() ,所以
,所以 ![]() ,
,
∵ ![]() ,
, ![]() ,
,
∴ ![]() 平面
平面 ![]() ,∵
,∵ ![]() ,∴
,∴ ![]() 平面
平面 ![]() ,∴
,∴ ![]() ,
,
所以在 ![]() 中,得
中,得 ![]()
在 ![]() 中,又
中,又 ![]() ,∴
,∴ ![]()
又 ![]() ,∴
,∴ ![]() 平面
平面 ![]() .
.
(2)解:取 ![]() 的中点
的中点 ![]() ,则
,则 ![]() ,由(1)知,
,由(1)知, ![]() 平面
平面 ![]() .
.
所以平面 ![]() 平面
平面 ![]() ,所以
,所以 ![]() 平面
平面 ![]() ,作
,作 ![]() ,垂足为
,垂足为 ![]() ,连接
,连接 ![]() ,
,
由三垂线定理知, ![]() ,
,
所以 ![]() 就是所求二面角
就是所求二面角 ![]() 的平面角.
的平面角.
在 ![]() 中,
中, ![]() ,
, ![]() ,
,
所以 ![]() ,所以
,所以 ![]() ,
,
所以二面角 ![]() 的余弦值为
的余弦值为 ![]() .
.
【解析】(1)平面图形的翻折问题中,要注意哪些因素改变,哪些因素不改变,由直线与平面图内两条相交直线都有垂直证明直线与平面垂直.
(2)先由二面角的定义找互二面角的一个平面图角,再在三角形中,通过解三角形求角.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】甲船在岛![]() 的正南方
的正南方![]() 处,
处,![]() 千米,甲船以每小时
千米,甲船以每小时![]() 千米的速度向正北航行,同时乙船自
千米的速度向正北航行,同时乙船自![]() 出发以每小时
出发以每小时![]() 千米的速度向北偏东
千米的速度向北偏东![]() 的方向驶去,当甲,乙两船相距最近时,它们所航行的时间是( )
的方向驶去,当甲,乙两船相距最近时,它们所航行的时间是( )
A. ![]() 分钟 B.
分钟 B. ![]() 分钟 C.
分钟 C. ![]() 分钟 D.
分钟 D. ![]() 分钟
分钟
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,圆的参数方程为 ![]() (φ为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,直线l的极坐标方程为
(φ为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,直线l的极坐标方程为 ![]() .
.
(1)将圆的参数方程化为普通方程,在化为极坐标方程;
(2)若点P在直线l上,当点P到圆的距离最小时,求点P的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
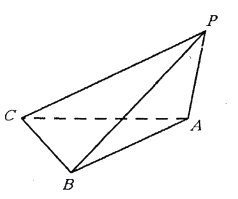
【题目】已知三棱锥 ![]() ,底面
,底面 ![]() 是以
是以 ![]() 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形, ![]() ,
, ![]() ,二面角
,二面角 ![]() 的大小为
的大小为 ![]() .
.
(1)求直线 ![]() 与平面
与平面 ![]() 所成角的大小;
所成角的大小;
(2)求二面角 ![]() 的正切值.
的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购买人数越少.把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元.现在这种羊毛衫的成本价是100元/ 件,商场以高于成本价的价格(标价)出售. 问:
(1)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(2)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com