
【题目】某班倡议假期每位学生至少阅读一本名著,为了解学生的阅读情况,对该班所有学生进行了调查.调查结果如下表:

(1)试根据上述数据,求这个班级女生阅读名著的平均本数;
(2)若从阅读5本名著的学生中任选2人交流读书心得,求选到男生和女生各1人的概率;
(3)试比较该班男生阅读名著本数的方差![]() 与女生阅读名著本数的方差
与女生阅读名著本数的方差![]() 的大小(只需写出结论).
的大小(只需写出结论).
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)运用平均数的计算公式求解即可;(2)运用列举法列出从阅读5本名著的5名学生中任取2人所有结果,以及其中男生和女生各1人的所有结果,然后利用古典概型公式求解即可;(3)直接计算出其方差并进行比较即可.
试题解析:(1)女生阅读名著的平均本数本![]() 本.………………3分
本.………………3分
(2)设事件![]() 从阅读5本名著的学生中任取2人,其中男生和女生各1人
从阅读5本名著的学生中任取2人,其中男生和女生各1人![]() .
.
男生阅读5本名著的3人分别记为![]() ,女生阅读5本名著的2人分别记为
,女生阅读5本名著的2人分别记为![]() .
.
从阅读5本名著的5名学生中任取2人,共有10个结果,分别是:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
其中男生和女生各1人共有6个结果,分别是:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
则![]() .……………………9分
.……………………9分
(3)![]() .………………12分
.………………12分


科目:高中数学 来源: 题型:
【题目】若有穷数列![]() (
(![]() 是正整数),满足
是正整数),满足![]() 即
即![]() (
(![]() 是正整数,且
是正整数,且![]() ),就称该数列为“对称数列”。例如,数列
),就称该数列为“对称数列”。例如,数列![]() 与数列
与数列![]() 都是“对称数列”.
都是“对称数列”.
(1)已知数列![]() 是项数为9的对称数列,且
是项数为9的对称数列,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列, ![]() ,
, ![]() ,试求
,试求![]() ,
, ![]() ,
, ![]() ,
, ![]() ,并求前9项和
,并求前9项和![]() .
.
(2)若![]() 是项数为
是项数为![]() 的对称数列,且
的对称数列,且![]() 构成首项为31,公差为
构成首项为31,公差为![]() 的等差数列,数列
的等差数列,数列![]() 前
前![]() 项和为
项和为![]() ,则当
,则当![]() 为何值时,
为何值时, ![]() 取到最大值?最大值为多少?
取到最大值?最大值为多少?
(3)设![]() 是
是![]() 项的“对称数列”,其中
项的“对称数列”,其中![]() 是首项为1,公比为2的等比数列.求
是首项为1,公比为2的等比数列.求![]() 前
前![]() 项的和
项的和![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ABC=60°,∠BAC=90°,AD是BC边上的高,沿AD将△ABC折成60°的二面角B-AD-C,如图2.
(1)证明:平面ABD⊥平面BCD;
(2)设E为BC的中点,BD=2,求异面直线AE与BD所成的角的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】语文成绩服从正态分布![]() ,数学成绩的频率分布直方图如下:
,数学成绩的频率分布直方图如下:

(I)如果成绩大于135的为特别优秀,这500名学生中本次考试语文、数学特别优秀的大约各多少人?(假设数学成绩在频率分布直方图中各段是均匀分布的)
(II)如果语文和数学两科都特别优秀的共有6人,从(I)中的这些同学中随机抽取3人,设三人中两科都特别优秀的有![]() 人,求
人,求![]() 的分布列和数学期望.
的分布列和数学期望.
(附参考公式)若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下:
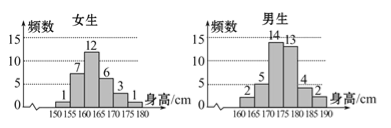
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm之间的概率;
(3)从样本中身高在180~190cm之间的男生中任选2人,求至少有1人身高在185~190cm之间的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是定义在R上的奇函数,且x<0时,f(x)=1+2x.
(1)求函数f(x)的解析式;
(2)画出函数f(x)的图像;
(3)写出函数f(x)的单调区间及值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,记二次函数
中,记二次函数![]() (
(![]() )与两坐标轴有三个交点,其中与x轴的交点为A,B.经过三个交点的圆记为
)与两坐标轴有三个交点,其中与x轴的交点为A,B.经过三个交点的圆记为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)设P为圆![]() 上一点,若直线PA,PB分别交直线
上一点,若直线PA,PB分别交直线![]() 于点M,N,则以MN为直径的圆是否经过线段AB上一定点?请证明你的结论.
于点M,N,则以MN为直径的圆是否经过线段AB上一定点?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】众所周知,乒乓球是中国的国球,乒乓球队内部也有着很严格的竞争机制,为了参加国际大赛,种子选手甲与三位非种子选手乙、丙、丁分别进行一场内部对抗赛,按以往多次比赛的统计,甲获胜的概率分别为![]() ,
,![]() ,
,![]() ,且各场比赛互不影响.
,且各场比赛互不影响.
(1)若甲至少获胜两场的概率大于![]() ,则甲入选参加国际大赛参赛名单,否则不予入选,问甲是否会入选最终的大名单?
,则甲入选参加国际大赛参赛名单,否则不予入选,问甲是否会入选最终的大名单?
(2)求甲获胜场次![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com