
| A. | sinx+ex | B. | cosx+ex | C. | -sinx+ex | D. | -cosx+ex |
分析 利用三角函数,指数函数,幂函数的导数公式分别进行求导,找出规律即可.
解答 解:f1(x)=f′(x)=cosx+ex+2013x2012
f2(x)=f′1(x)=-sinx+ex+2013×2012×x2011
f3(x)=f′2(x)=-cosx+ex+2013×2012×2011x2010
f4(x)=f′3(x)=sinx+ex+2013×2012×2011×2010x2009
…
f2013(x)=cosx+ex+2013!
f2014(x)=f′2013(x)=-sinx+ex
故选:C.
点评 本题考查基本初等函数的导数公式、考查通过不完全归纳找规律的推理方法,属基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲 | 79 | 74 | 88 | 97 | 90 | 82 |
| 乙 | 74 | 77 | 81 | 92 | 96 | 90 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
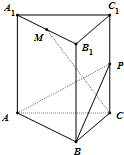 如图,直三棱柱ABC-A1B1C1的底面是边长为4正三角形,$A{A_1}=2\sqrt{6}$,M为A1B1的中点.
如图,直三棱柱ABC-A1B1C1的底面是边长为4正三角形,$A{A_1}=2\sqrt{6}$,M为A1B1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com