
【题目】函数![]() 的定义域为
的定义域为![]() ,且对任意
,且对任意![]() ,有
,有![]() ,且当
,且当![]() 时
时![]() .
.
(1)证明:![]() 是奇函数;
是奇函数;
(2)证明:![]() 在
在![]() 上是减函数;
上是减函数;
(3)求![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
【答案】(1)证明见解析;(2)证明见解析;(3) 最大值是6,最小值是-6.
【解析】
(1)令x=y=0,则可得f(0)=0;y=﹣x,即可证明f(x)是奇函数,
(2)设x1>x2,由已知可得f(x1﹣x2)<0,再利用f(x+y)=f(x)+f(y),及减函数的定义即可证明.
(3)由(2)的结论可知f(﹣3)、f(3)分别是函数y=f(x)在[﹣3、3]上的最大值与最小值,故求出f(﹣3)与f(3)就可得所求值域.
(1)因为![]() 的定义域为
的定义域为![]() ,且
,且![]() ,
,
令![]() 得
得![]() ,所以
,所以![]() ;
;
令![]() ,则
,则![]() ,所以
,所以![]() ,
,
从而有![]() ,所以
,所以![]() ,所以
,所以![]() 是奇函数.
是奇函数.
(2)任取![]() ,且
,且![]() ,
,
则![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() ,从而
,从而![]() 在
在![]() 上是减函数.
上是减函数.
(3)由于![]() 在
在![]() 上是减函数,
上是减函数,
故![]() 在区间
在区间![]() 上的最大值是
上的最大值是![]() ,最小值是
,最小值是![]() ,
,
由于![]() ,所以
,所以![]()
![]() ,
,
由于![]() 为奇函数知,
为奇函数知, ![]() ,
,
从而![]() 在区间
在区间![]() 上的最大值是6,最小值是
上的最大值是6,最小值是![]() 6.
6.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为了了解某城市居民用水量情况,我们抽取了100位居民某年的月均用水量(单位:吨)并对数据进行处理,得到该100位居民月均用水量的频率分布表,并绘制了频率分布直方图(部分数据隐藏).

(1)确定表中的![]() 与
与![]() 的值;
的值;
(2)在上述频率分布直方图中,求从左往右数第4个矩形的高度;
(3)在频率分布直方图中画出频率分布折线图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,命题
,命题![]() 方程
方程![]() 表示焦点在
表示焦点在![]() 轴上的椭圆,命题
轴上的椭圆,命题![]() 方程
方程![]() 表示双曲线.
表示双曲线.
(1)若命题![]() 是真命题,求实数
是真命题,求实数![]() 的范围;
的范围;
(2)若命题“![]() 或
或![]() ”为真命题,“
”为真命题,“![]() 且
且![]() ”是假命题,求实数
”是假命题,求实数![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.
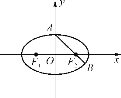
(1)若∠F1AB=90°,求椭圆的离心率;
(2)若![]() =2
=2![]() ,
,![]() ·
·![]() =
=![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海产品经销商调查发现,该海产品每售出![]() 吨可获利
吨可获利![]() 万元,每积压
万元,每积压![]() 吨则亏损
吨则亏损![]() 万元.根据往年的数据,得到年需求量的频率分布直方图如图所示,将频率视为概率.
万元.根据往年的数据,得到年需求量的频率分布直方图如图所示,将频率视为概率.
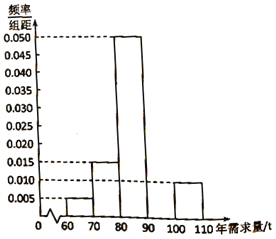
(1)请补齐![]() 上的频率分布直方图,并依据该图估计年需求量的平均数;
上的频率分布直方图,并依据该图估计年需求量的平均数;
(2)今年该经销商欲进货![]() 吨,以
吨,以![]() (单位:吨,
(单位:吨, ![]() )表示今年的年需求量,以
)表示今年的年需求量,以![]() (单位:万元)表示今年销售的利润,试将
(单位:万元)表示今年销售的利润,试将![]() 表示为
表示为![]() 的函数解析式;并求今年的年利润不少于
的函数解析式;并求今年的年利润不少于![]() 万元的概率.
万元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com