
【题目】已知函数![]() ,且
,且![]() .
.
(1)求f(x)的解析式;
(2)判断f(x)在区间(0,1)上的单调性,并用定义法证明.
【答案】(1)![]() (2)f(x)在(0,1)上单调递减,证明见解析.
(2)f(x)在(0,1)上单调递减,证明见解析.
【解析】
(1)根据![]() 即可求出a=b=1,从而得出
即可求出a=b=1,从而得出![]() ;
;
(2)容易判断f(x)在区间(0,1)上单调递减,根据减函数的定义证明:设x1,x2∈(0,1),并且x1<x2,然后作差,通分,得出![]() ,根据x1,x2∈(0,1),且x1<x2说明f(x1)>f(x2)即可.
,根据x1,x2∈(0,1),且x1<x2说明f(x1)>f(x2)即可.
解:(1)∵![]() ;
;
∴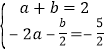 ;
;
解得a=1,b=1;
∴![]() ;
;
(2)f(x)在区间(0,1)上单调递减,证明如下:
设x1,x2∈(0,1),且x1<x2,则:
![]() =
=![]() ;
;
∵x1,x2∈(0,1),且x1<x2;
∴x1-x2<0,![]() ,
,![]() ;
;
∴![]() ;
;
∴f(x1)>f(x2);
∴f(x)在(0,1)上单调递减.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={x|2a+1≤x≤3a-5},B={x|x<-1,或x>16},分别根据下列条件求实数a的取值范围.
(1)A∩B=![]() ;(2)A(A∩B).
;(2)A(A∩B).
查看答案和解析>>
科目:高中数学 来源: 题型:
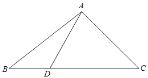
【题目】如图所示,在△ABC中,D是BC边上的一点,且AB=14,BD=6,∠ADC=![]() ,
,![]() .
.
(Ⅰ)求sin∠DAC;
(Ⅱ)求AD的长和△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心在直线![]() 上,且圆C与x轴交于两点
上,且圆C与x轴交于两点![]() ,
,![]() .
.
(1)求圆C的方程;
(2)已知圆M:![]() ,设
,设![]() 为坐标平面上一点,且满足:存在过点
为坐标平面上一点,且满足:存在过点![]() 且互相垂直的直线
且互相垂直的直线![]() 和
和![]() 有无数对,它们分别与圆C和圆M相交,且圆心C到直线
有无数对,它们分别与圆C和圆M相交,且圆心C到直线![]() 的距离是圆心M到直线
的距离是圆心M到直线![]() 的距离的2倍,试求所有满足条件的点
的距离的2倍,试求所有满足条件的点![]() 的坐标
的坐标
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,
(1)求函数![]() 的定义域;
的定义域;
(2)判断![]() 的奇偶性;
的奇偶性;
(3)方程![]() 是否有根?如果有根
是否有根?如果有根![]() ,请求出一个长度为
,请求出一个长度为![]() 的区间
的区间![]() ,使
,使![]() ;如果没有,请说明理由?(注:区间
;如果没有,请说明理由?(注:区间![]() 的长度
的长度![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数(简称:![]() )是定量描述空气质量状况的无量纲指数,空气质量按照
)是定量描述空气质量状况的无量纲指数,空气质量按照![]() 大小分为六级:
大小分为六级:![]() 为优,
为优,![]() 为良,
为良,![]() 为轻度污染,
为轻度污染,![]() 为中度污染,
为中度污染,![]() 为重度污染,
为重度污染,![]() 为严重污染.下面记录了北京市
为严重污染.下面记录了北京市![]() 天的空气质量指数,根据图表,下列结论错误的是( )
天的空气质量指数,根据图表,下列结论错误的是( )

A. 在北京这![]() 天的空气质量中,按平均数来考察,最后
天的空气质量中,按平均数来考察,最后![]() 天的空气质量优于最前面
天的空气质量优于最前面![]() 天的空气质量 B. 在北京这
天的空气质量 B. 在北京这![]() 天的空气质量中,有
天的空气质量中,有![]() 天达到污染程度
天达到污染程度
C. 在北京这![]() 天的空气质量中,12月29日空气质量最好 D. 在北京这
天的空气质量中,12月29日空气质量最好 D. 在北京这![]() 天的空气质量中,达到空气质量优的天数有
天的空气质量中,达到空气质量优的天数有![]() 天
天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日是第二十七届“世界水日”,
日是第二十七届“世界水日”,![]() 月
月![]() 日是第三十二届“中国水周”.我国纪念
日是第三十二届“中国水周”.我国纪念![]() 年“世界水日”和“中国水周”活动的宣传主题为“坚持节水优先,强化水资源管理”.某中学课题小组抽取
年“世界水日”和“中国水周”活动的宣传主题为“坚持节水优先,强化水资源管理”.某中学课题小组抽取![]() 、
、![]() 两个小区各
两个小区各![]() 户家庭,记录他们
户家庭,记录他们![]() 月份的用水量(单位:
月份的用水量(单位:![]() )如下表:
)如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据两组数据完成下面的茎叶图,从茎叶图看,哪个小区居民节水意识更好?
|
| |
| ||
| ||
| ||
|
(2)从用水量不少于![]() 的家庭中,
的家庭中,![]() 、
、![]() 两个小区各随机抽取一户,求
两个小区各随机抽取一户,求![]() 小区家庭的用水量低于
小区家庭的用水量低于![]() 小区的概率.
小区的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 对一切实数
对一切实数![]() ,
,![]() 都有
都有![]() 成立,且
成立,且![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式;
的解析式;
(3)已知![]() ,设
,设![]() :当
:当![]() 时,不等式
时,不等式![]() 恒成立;
恒成立;![]() :当
:当![]() 时,
时,![]() 是单调函数.如果满足
是单调函数.如果满足![]() 成立的
成立的![]() 的集合记为
的集合记为![]() ,满足
,满足![]() 成立的
成立的![]() 的集合记为
的集合记为![]() ,求
,求![]() (
(![]() 为全集).
为全集).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com