
某工厂有工人 人,其中
人,其中 名工人参加过短期培训(称为
名工人参加过短期培训(称为 类工人),另外
类工人),另外 名工人参加过长期培训(称为
名工人参加过长期培训(称为 类工人).现用分层抽样的方法(按
类工人).现用分层抽样的方法(按 类、
类、 类分二层)从该工厂的工人中共抽查
类分二层)从该工厂的工人中共抽查  名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
(1) 类工人和
类工人和 类工人中各抽查多少工人?
类工人中各抽查多少工人?
(2)从 类工人中的抽查结果和从
类工人中的抽查结果和从 类工人中的抽查结果分别如下表1和表2.
类工人中的抽查结果分别如下表1和表2.
表1
生产能力分组 |
|
|
|
|
|
人数 |
|
|
|
|
|
表2
生产能力分组 |
|
|
|
|
人数 |
|
|
|
|


①求 、
、 ,再完成下列频率分布直方图;
,再完成下列频率分布直方图;
②分别估计 类工人和
类工人和 类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组
类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组
中的数据用该组区间的中点值作代表).
(1)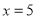 ,
,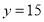 ;(2)详见解析;(3)
;(2)详见解析;(3)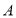 类工人、
类工人、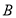 类工人以及该厂工人的生产能力的平均数分别为
类工人以及该厂工人的生产能力的平均数分别为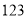 、
、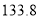 、
、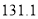 .
.
【解析】
试题分析:(1)根据分层抽样中各层的入样比与总体的抽样比相等求出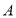 类工人和
类工人和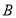 类工人中抽查的工人数;(2)①在(1)中的条件下,利用
类工人中抽查的工人数;(2)①在(1)中的条件下,利用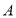 类工人和
类工人和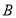 类工人所抽查的工人总数求出
类工人所抽查的工人总数求出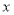 、
、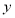 的值;②在频率分布直方图中,利用每组的区间的中点值乘以相应组的频率的乘积相加的方法求出
的值;②在频率分布直方图中,利用每组的区间的中点值乘以相应组的频率的乘积相加的方法求出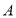 类工人和
类工人和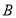 类工人的生产能力的平均数,然后再将
类工人的生产能力的平均数,然后再将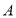 类工人和
类工人和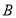 类工人生产能力平均数分别乘以
类工人生产能力平均数分别乘以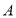 类工人和
类工人和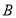 类工人的百分比的乘积相加的到该厂工人生产能力的平均数.
类工人的百分比的乘积相加的到该厂工人生产能力的平均数.
试题解析:(1)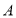 类工人和
类工人和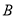 类工人中分别抽查
类工人中分别抽查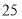 名和
名和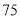 名;
名;
(2)①由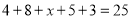 ,得
,得 ,
,
由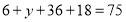 ,得
,得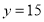 .频率分布直方图如下:
.频率分布直方图如下:
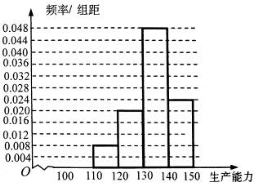
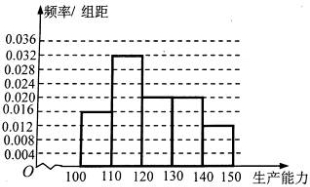
②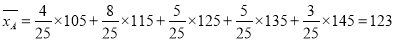 ,
,
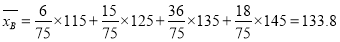 ,
,
 ,
,
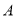 类工人生产能力的平均数,
类工人生产能力的平均数,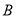 类工人生产能力的平均数以及该工厂工人生产能力的平均数的估计值分别为
类工人生产能力的平均数以及该工厂工人生产能力的平均数的估计值分别为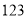 、
、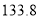 、
、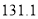 .
.
考点:1.分层抽样;2.频率分布直方图中平均数的计算


科目:高中数学 来源:2013-2014学年广东省韶关市高三4月高考模拟(二模)文科数学试卷(解析版) 题型:选择题
在某次测量中得到的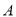 样本数据如下:82、84、84、86、86、86、88、88、88、88.若
样本数据如下:82、84、84、86、86、86、88、88、88、88.若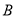 样本数据恰好是
样本数据恰好是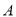 样本数据每一个数都加2后所得数据,则
样本数据每一个数都加2后所得数据,则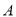 、
、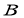 两个样本的下列数字特征对应相同的是( )
两个样本的下列数字特征对应相同的是( )
A.众数 B.平均数 C.中位数 D.方差
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省湛江市高三高考模拟测试二理科数学试卷(解析版) 题型:选择题
对于任意两个正整数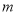 、
、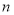 ,定义某种运算“※”,法则如下:当
,定义某种运算“※”,法则如下:当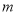 、
、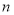 都是正奇数时,
都是正奇数时,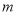 ※
※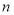 =
=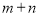 ;当
;当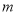 、
、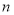 不全为正奇数时,
不全为正奇数时,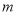 ※
※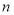 =
=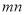 .则在此定义下,集合
.则在此定义下,集合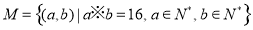 中的元素个数是( )
中的元素个数是( )
A.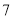 B.
B.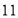 C.
C.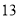 D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省湛江市高三高考模拟测试二理科数学试卷(解析版) 题型:选择题
在复平面内,复数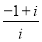 对应的点位于( )
对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省湛江市高三高考模拟测试二文科数学试卷(解析版) 题型:填空题
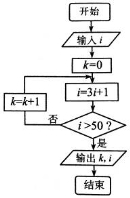
阅读如图所示的程序框图,若输入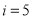 ,则输出的
,则输出的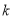 值为______________.
值为______________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省汕头市高三3月高考模拟考试文科试卷(解析版) 题型:选择题
“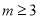 ”是“关于
”是“关于 、
、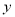 的不等式组
的不等式组 表示的平面区域为三角形”的( )
表示的平面区域为三角形”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省梅州市高三3月总复习质检文科数学试卷(解析版) 题型:选择题
若直角坐标平面内的亮点P,Q满足条件: P,Q都在函数y=f(x)的图像上, P,Q关于原点对称,则称点对[P,Q]是函数y=f(x)的一对“友好点对”(点对[P,Q]与[Q,P]看作同一对“友好点对”)。
已知函数 ,则此函数的“友好点对”有( )
,则此函数的“友好点对”有( )
A.0对 B.1对 C.2对 D.3对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com